Question

【题目】如图，已知正方形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，抛物线y=x2+bx+c经过点A，B，交正x轴于点D，E是OC上的动点（不与C重合）连接EB，过B点作BF⊥BE交y轴与F

（1）求b，c的值及D点的坐标；

（2）求点E在OC上运动时，四边形OEBF的面积有怎样的规律性？并证明你的结论；

（3）连接EF，BD，设OE=m，△BEF与△BED的面积之差为S，问：当m为何值时S最小，并求出这个最小值．

Answer 1

【答案】（1）b=，c=2；D点坐标为（3，0）．（2）点E在OC上运动时，四边形OEBF的面积不变；（3）当m=2﹣时S最小为0．

【解析】

试题分析：（1）把点A，B代入抛物线y=x2+bx+c求得b、c即可，y=0，建立方程求得点D；

（2）四边形OEBF的面积不变，利用三角形全等证得结论即可；

（3）用m分别表示出两个三角形的面积，求差探讨得出答案即可．

试题解析：（1）把点A（0，2）、B（2，2）代入抛物线y=x2+bx+c得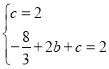

解得b=，c=2；

∴y=x2+x+2；

令x2+x+2=0

解得x1=﹣1，x2=3

∴D点坐标为（3，0）．

（2）点E在OC上运动时，四边形OEBF的面积不变；

∵四边形OABC是正方形

∴AB=BC，∠BCE=∠BAE=∠ABC=90°

又∵BF⊥BE

∴∠FBE=90°

∴∠ABF=∠CBE

∴△ABF≌△BCE

∴四边形OEBF的面积始终等于正方形OABC的面积．

（3）如图，

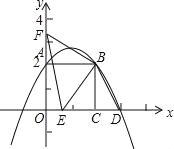
可以看出S△BEF=S梯形OCBF﹣S△OEF﹣S△BEC

=（2+2+m）×2﹣m（2+m）﹣（2﹣m）×2

=﹣m2+m+2

S△BED=×（3﹣m）×2

=3﹣m

两个三角形的面积差最小为0，

即3﹣m=﹣m2+m+，

解得m=2±，

∵E是OC上的动点

∴m=2﹣，

当m=2﹣时S最小为0．