题目内容
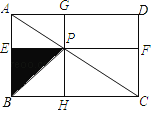
【题目】如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，GH∥AB．分别交AB、CD、AD、BC于E、F、G、H，连接PB．若AE＝3，PF＝8．则图中阴影部分的面积为（ ）
A.8B.12C.16D.24
【答案】B
【解析】
注意到易证得△AEP∽△CFP，则有
，整理得，FCPE=AEPF=8×3=24，而阴影部分的面积为
BEPE，由四边形ABCD为矩形，则BE=FC，即阴影部分的面积为FCPE=×24=12，即为答案．
∵四边形ABCD是矩形
∴AB∥CD
∴∠EAP＝∠FCP，∠AEP=∠CFP
∴△AEP∽△CFP
∴
∴FCPE＝AEPF＝8×3＝24
∵EF∥BC
∴四边形EFCB为矩形
∴EB＝FC
∵阴影部分的面积为BEPE
∴阴影部分的面积为BEPE＝FCPE＝×24＝12
故选：B．
练习册系列答案
中考解读考点精练系列答案
相关题目
