题目内容
【题目】我们定义：如果一个等腰三角形有一条边长是3，那么这个三角形称作帅气等腰三角形.已知
中，
，
，
，在所在平面内画一条直线，将分割成两个三角形，若其中一个三角形是帅气等腰三角形，则这样的直线最多可画（ ）
A.0条B.1条C.2条D.3条
【答案】B
【解析】
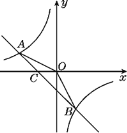
先根据各边的长度画出三角形ABC，作AD⊥BC，根据勾股定理求出AD，BD，结合图形可分析出结果.
已知如图，所做三角形是钝角三角形，作AD⊥BC，
根据勾股定理可得：AC2-CD2=AB2-BD2
所以设CD=x,则BD=7-x
所以52-x2=（
）2-（7-x）2
解得x=4
所以CD=4,BD=3,
所以，在直角三角形ADC中
AD=
所以AD=BD=3
所以三角形ABD是帅气等腰三角形
假如从点C或B作直线，不能作出含有边长为3的等腰三角形
故符合条件的直线只有直线AD
故选：B
练习册系列答案
名校课堂系列答案
相关题目
【题目】某大型超市投入15000元资金购进
、
两种品牌的矿泉水共600箱，矿泉水的成本价和销售价如下表所示：
类别/单价 | 成本价（元/箱） | 销售价（元/箱） |
A品牌 | 20 | 32 |
B品牌 | 35 | 50 |
（1）该大型超市购进、品牌矿泉水各多少箱？
（2）全部销售完600箱矿泉水，该超市共获得多少利润？
