题目内容
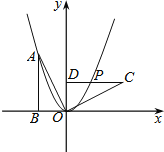
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是( )
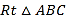
A.1.5B.1.8C.2D.2.5
【答案】A
【解析】
连接DF,由勾股定理求出AB=5,由等腰三角形的性质得出CE=DE,由线段垂直平分线的性质得出CF=DF,由SSS证明△ADF≌△ACF,得出∠ADF=∠ACF=∠BDF=90°,设CF=DF=x,则BF=4-x,在Rt△BDF中,由勾股定理得出方程,解方程即可.
解:连接DF,如图所示:
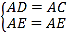
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴![]()
∵AD=AC=3,AF⊥CD,
∴CE=DE,BD=AB-AD=2,∴CF=DF,
在△ADF和△ACF中,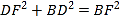
∴△ADF≌△ACF(SSS),
∴∠ADF=∠ACF=90°,
∴∠BDF=90°,
设CF=DF=x,则BF=4-x,
在Rt△BDF中,由勾股定理得: ![]() ,
,
即![]() ,
,
解得:x=1.5;
∴CF=1.5;
故选:A.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
销售量p(件) | P=50—x |
销售单价q(元/件) | 当1≤x≤20时,q=30+ 当21≤x≤40时,q=20+ |
(1)求该网店第x天获得的利润y关于x的函数关系式;
(2)这40天中该网店第几天获得的利润最大?最大利润是多少?