Question

【题目】如图，在平面直角坐标系中，点的坐标是，动点从原点O出发，沿着轴正方向移动，以为斜边在第一象限内作等腰直角三角形，设动点的坐标为.

(1)当时，点的坐标是 ；当时，点的坐标是 ；

(2)求出点的坐标(用含的代数式表示)；

(3)已知点的坐标为，连接、，过点作轴于点，求当为何值时，当与全等.

Answer 1

【答案】(1) (2，2)；(，)； (2) P(，)；(3) .

【解析】

(1) 当时，三角形AOB为等腰直角三角形， 所以四边形OAPB为正方形，直接写出结果；当时，作PN⊥y轴于N，作PM⊥x轴与M，求出△BNP≌△AMP，即可得到ON+OM=OB-BN+OA+AM=OB+OA，即可求出；

(2) 作PE⊥y轴于E，PF⊥x轴于F，求出△BEP≌△AFP，即可得到OE+OF=OB+BE+OA+AF=OB+OA，即可求出；

(3) 根据已知求出BC值，根据上问得到OQ= ，△PQB≌△PCB，BQ=BC，因为OQ=BQ+OB，即可求出t.

(1) 当时，三角形AOB为等腰直角三角形如图

所以四边形OAPB为正方形，所以P(2，2)

当时，如图

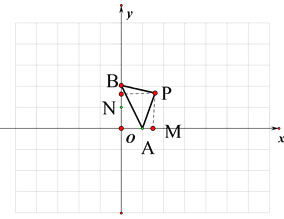
作PN⊥y轴于N，作PM⊥x轴与M

∴四边形OMPN为矩形

∵∠BPN+∠NPA=∠APM+∠NPA=90°

∴ ∠BPN =∠APM

∵∠BNP=∠AMP

∴ △BNP≌△AMP

∴PN=PM BN=AM

∴四边形OMPN为正方形，OM=ON=PN=PM

∴ON+OM=OB-BN+OA+AM=OB+OA=2+1=3

∴OM=ON=PN=PM=

∴ P(，)

(2) 如图

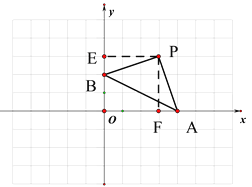
作PE⊥y轴于E，PF⊥x轴于F，则四边形OEPF为矩形

∵∠BPE+∠BPF=∠APF+∠BPF=90°

∴ ∠BPE =∠APF

∵∠BEP=∠AFP

∴ △BEP≌△AFP

∴PE=PF BE=AF

∴四边形OEPF为正方形，OE=OF=PE=PF

∴OE+OF=OB+BE+OA+AF=OB+OA=2+t

∴ OE=OF=PE=PF=

∴ P(，)；

(3) 根据题意作PQ⊥y轴于Q，作PG⊥x轴与G

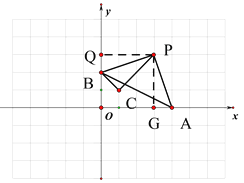
∵ B(0，2) C(1，1)

∴ BC=

由上问可知P(，)，OQ=

∵△PQB≌△PCB

∴BC=QB=

∴ OQ=BQ+OB=+2=

解得 t=.