Question

【题目】如图，在△ABC中，∠ACB=α（90°＜α＜180°），将△ABC绕着点A逆时针旋转2β（0°＜β＜90°）后得△AED，其中点E、D分别和点B、C对应，联结CD，如果CD⊥ED，请写出一个关于α与β的等量关系的式子 ．

Answer 1

【答案】α+β=180°
【解析】解：如图，过A作AF⊥CD，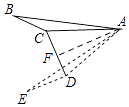
由旋转可得，∠ADE=∠ACB=α，
∵CD⊥DE，
∴∠ADC=α﹣90°，
由旋转可得，AC=AD，∠CAD=2β，
∴∠DAF=β，
∴Rt△ADF中，∠DAF+∠ADF=90°，即β+α﹣90°=90°，
∴α+β=180°．
所以答案是：α+β=180°．
【考点精析】本题主要考查了三角形的内角和外角和等腰三角形的性质的相关知识点，需要掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；等腰三角形的两个底角相等（简称：等边对等角）才能正确解答此题．