��Ŀ����
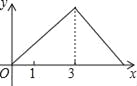
����Ŀ����ͼ���ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ������Ϊ��0��6������
��������0��6������![]() ��������4��0������
������Ϊ��4��0������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��2����λ���ȵ��ٶ����
��ÿ��2����λ���ȵ��ٶ����![]() ������ͬʱ��
������ͬʱ��![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��3����λ���ȵ��ٶ����
��ÿ��3����λ���ȵ��ٶ����![]() �˶�������
�˶�������![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() ��
��![]() ͬʱֹͣ�˶������˶�ʱ��Ϊ
ͬʱֹͣ�˶������˶�ʱ��Ϊ![]() �룮
�룮
��1����![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() �����Ϊ_____________��
�����Ϊ_____________��
��2����![]() ��
��![]() ����ʱ����
����ʱ����![]() ��ֵ��
��ֵ��
��3��������������![]() ��ͼ����
��ͼ����![]() ��
��![]() ����ʱ��
����ʱ��
����![]() ��ֵ��
��ֵ��
�ڵ�![]() ��
��![]() ���ϣ���
���ϣ���![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ����Ե�
��ͼ���ϣ����Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ƽ���ı��Σ���ֱ��д����������������
Ϊ������ı�����ƽ���ı��Σ���ֱ��д����������������![]() �����꣮
�����꣮

���𰸡���1��3����2��![]() ��
��![]() ����3����
����3����![]() ����
����![]()
��������
��1��BP=4-2t��BQ=3t����t=1���������������������ʽ��ü���.
��2����![]() ʱ�����֢�
ʱ�����֢�![]() ����
����![]() ����������.
����������.
��3���ٽ�![]() ��
��![]() ����
����![]() ���ɵ�k.�ڸ���ƽ���ı��ε����ʣ�P��Q�����������IJ����M��N��������IJ���췽�����
���ɵ�k.�ڸ���ƽ���ı��ε����ʣ�P��Q�����������IJ����M��N��������IJ���췽�����
�⣺��1��BP=4-2t��BQ=3t����t=1ʱ�����������Ϊ![]() =3.
=3.
��2���ٵ�![]() ʱ����
ʱ����![]()
��![]() ��
��![]() ��
��![]()
![]()
��![]()
�ڵ�![]() ʱ����
ʱ����![]()
��![]() ��
��![]()
��![]() ��
��![]() ���������⣬��ȥ��
���������⣬��ȥ��
���ϣ�![]() ��
��![]()
��3���١�![]() ��
��![]()
�� ��
��![]() ��
��![]()
��
���ݢ���k=12,t=1,P(2,6),Q(4,3)
��M������Ϊ(x,0),N(a,![]() )
)
����ƽ���ı��ε����ʣ�P��Q�����������IJ����M��N��������IJ���췽����⣬
x-4=2-a,3=![]() -6,
-6,
���a=![]() ,x=
,x=![]() .
.
����M������Ϊ![]()

 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�