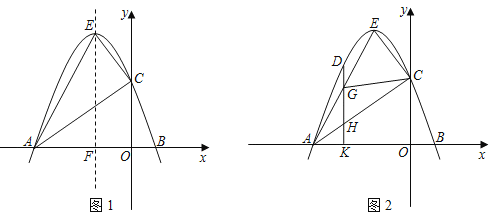ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΘ®Έ ΧβΧΫΨΩΘ©
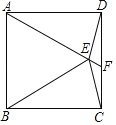
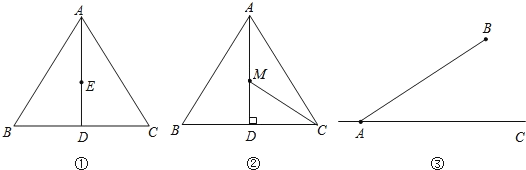
(1)»γΆΦΔΌΘ§ΒψE «’ΐΓςABCΗΏAD…œΒΡ“ΜΕ®Βψ,«κ‘ΎAB…œ’““ΜΒψFΘ§ ΙEF=![]() AEΘ§≤ΔΥΒΟςάμ”…ΘΜ
AEΘ§≤ΔΥΒΟςάμ”…ΘΜ
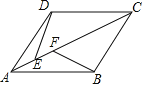
(2)»γΆΦΔΎΘ§ΒψM «±Ώ≥ΛΈΣ2ΒΡ’ΐΓςABCΗΏAD…œΒΡ“ΜΕ·ΒψΘ§«σ![]() AM+MCΒΡΉν–Γ÷ΒΘΜ
AM+MCΒΡΉν–Γ÷ΒΘΜ
Θ®Έ ΧβΫβΨωΘ©
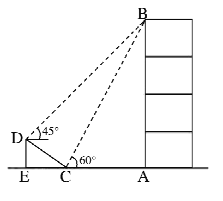
(3)»γΆΦΔέΘ§AΓΔBΝΫΒΊœύΨύ600km,AC «± ÷±ΒΊ―ΊΕΪΈςΖΫœρœρΝΫ±Ώ―”…λΒΡ“ΜΧθΧζ¬ΖΘ§ΒψBΒΫACΒΡΉνΕΧΨύάκΈΣ360kmΘ°ΫώΦΤΜ°‘ΎΧζ¬ΖœΏAC…œ–ό“ΜΗω÷–ΉΣ’ΨMΘ§‘Ό‘ΎBMΦδ–ό“ΜΧθ± ÷±ΒΡΙΪ¬ΖΓΘ»γΙϊΆ§―υΒΡΈοΉ ‘ΎΟΩ«ßΟΉΙΪ¬Ζ…œΒΡ‘ΥΖ― «Χζ¬Ζ…œΒΡΝΫ±ΕΓΘΡ«Ο¥Θ§ΈΣ ΙΆ®ΙΐΧζ¬Ζ”…AΒΫM‘ΌΆ®ΙΐΙΪ¬Ζ”…MΒΫBΒΡΉή‘ΥΖ―¥οΒΫΉν–Γ÷ΒΘ§«κ»ΖΕ®÷–ΉΣ’ΨMΒΡΈΜ÷Ο,≤Δ«σ≥ωAMΒΡ≥ΛΘ°(ΫαΙϊ±ΘΝτΗυΚ≈)
ΓΨ¥πΑΗΓΩΘ®1Θ©œξΦϊΫβΈωΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©AM=(480
ΘΜΘ®3Θ©AM=(480![]() )kmΘ°
)kmΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ωΓœBAD=30ΓψΘ§ΒΟ≥ωEF=![]() AEΘΜ
AEΘΜ
Θ®2Θ©ΗυΨίΧβ“βΒΟ≥ωCΘ§MΘ§N‘Ύ“ΜΧθ÷±œΏ…œ ±Θ§¥Υ ±![]() AM+MCΉν–ΓΘ§ΫχΕχ«σ≥ωΦ¥Ω…ΘΜ
AM+MCΉν–ΓΘ§ΫχΕχ«σ≥ωΦ¥Ω…ΘΜ
Θ®3Θ©ΉςBDΓΆACΘ§¥ΙΉψΈΣΒψDΘ§‘ΎAC“λ”ΎΒψBΒΡ“Μ≤ύΉςΓœCAN=30ΓψΘ§ΉςBFΓΆANΘ§¥ΙΉψΈΣΒψFΘ§ΫΜAC”ΎΒψMΘ§ΒψMΦ¥ΈΣΥυ«σΘ§‘ΎRtΓςABD÷–Θ§«σ≥ωADΒΡ≥ΛΘ§‘ΎRtΓςMBD÷–Θ§ΒΟ≥ωMDΒΡ≥ΛΘ§Φ¥Ω…ΒΟ≥ω¥πΑΗΘ°
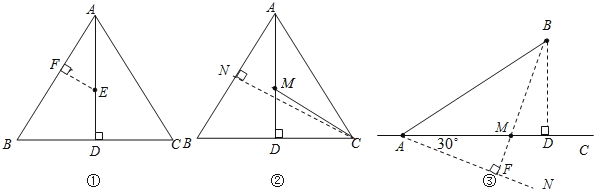
ΫβΘΚ(1)»γΆΦΔΌΘ§ΉςEFΓΆABΘ§¥ΙΉψΈΣΒψFΘ§ΒψFΦ¥ΈΣΥυ«σΓΘ
άμ”…»γœ¬ΘΚΓΏΒψE «’ΐΓςABCΗΏAD…œΒΡ“ΜΕ®ΒψΘ§
ΓύΓœBAD=30Θ§
ÿEFâABȧ
ΓύEF=![]() AEΘΜ
AEΘΜ
(2)»γΆΦΔΎ,ΉςCNΓΆAB,¥ΙΉψΈΣΒψN,ΫΜAD”ΎΒψM,¥Υ ±![]() AM+MCΉν–ΓΘ§Ήν–ΓΈΣCNΒΡ≥ΛΓΘ
AM+MCΉν–ΓΘ§Ήν–ΓΈΣCNΒΡ≥ΛΓΘ
ΓΏΓςABC «±Ώ≥ΛΈΣ2ΒΡ’ΐΓςABCΘ§
ΓύCN=BCsin60=2ΓΝ![]() =
=![]()
ΓύMN+CM=12AM+MC=![]()
Φ¥![]() AM+MCΒΡΉν–Γ÷ΒΈΣ
AM+MCΒΡΉν–Γ÷ΒΈΣ![]()
(3)»γΆΦΔέ,ΉςBDΓΆAC,¥ΙΉψΈΣΒψD,‘ΎAC“λ”ΎΒψBΒΡ“Μ≤ύΉςΓœCAN=30![]()
ΉςBFΓΆANΘ§¥ΙΉψΈΣΒψFΘ§ΫΜAC”ΎΒψMΘ§ΒψMΦ¥ΈΣΥυ«σΓΘ
‘ΎRtΓςABD÷–,AD=![]() (km)
(km)
‘ΎRtΓςMBD÷–,ΓœMBD=ΓœMAF=30,ΒΟMD=BDtan30=![]() (km)Θ§
(km)Θ§
Υυ“‘AM=(480![]() )kmΘ°
)kmΘ°