Question

【题目】如图，已知△ABC为等边三角形（三条边相等三个角为60°的三角形），点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．

（1）求证：△ABE≌△CAD；

（2）求∠BFD的度数．

Answer 1

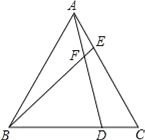
【答案】（1）见解析；（2）60°．

【解析】试题分析：（1）根据等边三角形的性质根据SAS即可证明△ABE≌△CAD；

（2）由三角形全等可以得出∠ABE=∠CAD，由外角与内角的关系就可以得出结论．

试题解析：（1）∵△ABC为等边三角形，

∴AB=BC=AC，∠ABC=∠ACB=∠BAC=60°．

在△ABE和△CAD中，

AB=CA， ∠BAC=∠C，AE =CD，

∴△ABE≌△CAD（SAS），

（2）∵△ABE≌△CAD，

∴∠ABE=∠CAD，

∵∠BAD+∠CAD=60°，

∴∠BAD+∠EBA=60°，

∵∠BFD=∠ABE+∠BAD，

∴∠BFD=60°．