题目内容
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:
①DA平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB; ④BE+AC=AB,其中正确的是( )
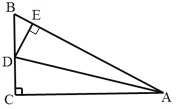
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】根据题中条件,结合图形及角平分线的性质得到:
∵AD平分∠BAC
∴∠DAC=∠DAE
∵∠C=90°,DE⊥AB
∴∠C=∠E=90°
∵AD=AD
∴△DAC≌△DAE
∴∠CDA=∠EDA
∴①AD平分∠CDE正确;
无法证明∠BDE=60°,
∴③DE平分∠ADB错误;
∵BE+AE=AB,AE=AC
∴BE+AC=AB
∴④BE+AC=AB正确;
∵∠BDE=90°-∠B,∠BAC=90°-∠B
∴∠BDE=∠BAC
∴②∠BAC=∠BDE正确.
故选:B.

练习册系列答案
相关题目



