题目内容
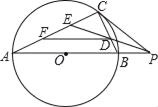
【题目】如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,![]() 恰好经过点O,则
恰好经过点O,则![]() 与
与![]() 的关系是
的关系是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
【答案】A
【解析】分析:
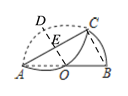
如下图,连接BC,过点O作OD⊥AC交半圆O于点D,交AC于点E,由此可得∠AEO=90°,OA=OD,由折叠的性质可得OE=DE=![]() OD=
OD=![]() OA,从而可得∠OAC=30°,进而可得∠ABC=60°,由此即可得到
OA,从而可得∠OAC=30°,进而可得∠ABC=60°,由此即可得到![]() .
.
详解:
如下图,连接BC,过点O作OD⊥AC交半圆O于点D,交AC于点E,
∴∠AEO=90°,OA=OD,
又∵由折叠的性质可得OE=DE=![]() OD=
OD=![]() OA,
OA,
∴∠BAC=30°,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠ABC=60°,
∴∠ABC=2∠ACB,
∴![]() .
.
故选A.

练习册系列答案
相关题目