��Ŀ����
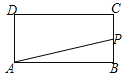
����Ŀ����ͼ����ֱ������ABCD�У�AD��BC����B=90�㣬AD=6cm��AB=8cm��BC=14cm������P��Q���ӵ�C��������P��C��B�����������˶�����Q��C��D��A�����������˶�����P��Q����һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶��� 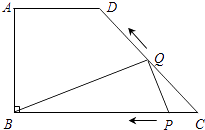
��1����CD�ij���
��2������P��1cm/s�ٶ��˶�����Q��2 ![]() cm/s���ٶ��˶�������BQ��PQ�����BQP���ΪS��cm2������P��Q�˶���ʱ��Ϊt��s������S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
cm/s���ٶ��˶�������BQ��PQ�����BQP���ΪS��cm2������P��Q�˶���ʱ��Ϊt��s������S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3������P���ٶ�����1cm/s����Q���ٶ�Ϊacm/s��Ҫʹ���˶������г���PQ��DC������ֱ��д��a��ȡֵ��Χ��
���𰸡�
��1���⣺��D����DH��BC������Ϊ��H��
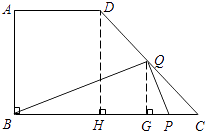
����DH=AB=8cm��BH=AD=6cm��
��CH=BC��BH=14��6=8cm��
��Rt��DCH�У���DHC=90�㣬
��CD= ![]() =8
=8 ![]() cm��
cm��
��2���⣺����P��Q�˶���ʱ��Ϊt��s������PC=t��
�� ����Q��CD��ʱ����Q����QG��BC������Ϊ��G����QC=2 ![]() t��
t��
�֡�DH=HC��DH��BC��
���C=45�㣮
����Rt��QCG��QG=QCsin��C=2 ![]() t��sin45��=2t��
t��sin45��=2t��
�֡�BP=BC��PC=14��t��
��S��BPQ= ![]() BP��QG=
BP��QG= ![]() ��14��t����2t=14t��t2��
��14��t����2t=14t��t2��
��Q�˶���D��ʱ����Ҫ��ʱ��t= ![]() =
= ![]() =4��
=4��
��S=14t��t2��0��t��4����
�ڵ���Q��DA��ʱ����Q����QG��BC������Ϊ��G��
��QG=AB=8cm��BP=BC��PC=14��t��
��S��BPQ= ![]() BP��QG=
BP��QG= ![]() ��14��t����8=56��4t��
��14��t����8=56��4t��
��Q�˶���A��ʱ����Ҫ��ʱ��t= ![]() =
= ![]() =4+
=4+ ![]() ��
��
��S=56��4t��4��t��4+ ![]() ����
����
�ۺ�����������ĺ�����ϵʽ�ǣ�
S=14t��t2��0��t��4����
S=56��4t��4��t��4+ ![]() ����
����
��3���⣺Ҫʹ�˶������г���PQ��DC��
��AD��BC����CPQD��ƽ���ı��Σ�
��CP=DQ��
1t=at��8 ![]() ��
��
��t= ![]() �٣�
�٣�
�֡�Q����AD���ϣ�
�� ![]() ��t��
��t�� ![]() �ڣ�
�ڣ�
�Ѣٴ���ڣ����a��1+ ![]() ��
��
��a��ȡֵ��Χ��a��1+ ![]() ��
��
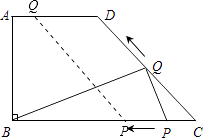
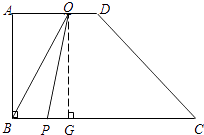
����������1����D����DH��BC������Ϊ��H������Rt��DCH�У���DH��CH�ij��ȣ����ù��ɶ����������CD�ij�����2�����ڵ�P���߶�CB���˶�������Q��C��D��A�����������˶������Է�����������ۣ��ٵ�Q��CD�ϣ��ڵ�Q��DA�ϣ����ÿһ������������Թ�Q����QG��BC��G�����ڵ�P��Q�˶���ʱ��Ϊt��s�������ú�t�Ĵ���ʽ�ֱ��ʾBP��QG�ij��ȣ�Ȼ����������ε������ʽ�������S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ����3����DQ=CP��Q����AD���ϣ����a��ȡֵ��Χ��
�����㾫����������Ҫ�����˹��ɶ����ĸ����ֱ�����ε����֪ʶ�㣬��Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��һ����ֱ�ڵ�������ֱ�����β�����ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�