题目内容
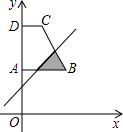如图，直角梯形ABCD中，AB∥CD，∠DAB=90°，顶点A的坐标是（0，2），点B、C、D的坐标分别是（2，2）、（1，4）、（0，4），一次函数y=x+t的图象l随t的不同取值变化时，位于l的右下方由l和梯形的边围成的图形面积为S（阴影部分）．则能反映S与t（0≤t＜4）之间的函数图象是（ ）A、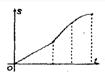 | B、 | C、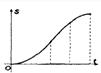 | D、 |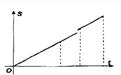
分析：如图，设直线y=x+t与AB交于E，交BC于F，交OA于G，由于B、C两点坐标已知，利用待定系数法可以求出直线BC的解析式，然后利用解析式可以求出BC与l的交点F的坐标，接着根据坐标可以分别表示FH，EB的长度，再利用三角形的面积公式就可以求出由l和梯形的边围成的图形面积为S（阴影部分），此题的面积有三种情况，第一种情况的函数关系式是二次函数，根据选择项就可以判定答案，不需要求出后两种情况．
解答：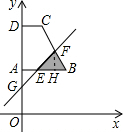
解：如图，设直线y=x+t与AB交于E，交BC于F，交OA于G，
∵B（2，2）、C（1，4）、
∴直线BC的解析式为y=-2x+6，
依题意得
，
∴
，
∴FH=
-2=
，
∵直线y=x+t，∴∠AGE=45°，
∴当y=0时，x=t，
∴OG=t，
∴AG=2-t，
∴AE=2-t，BE=t，
∴S△EFB=
×
×t=
t2，是关于t的二次函数，
图象应该是抛物线的一部分，
所给四个答案只有C正确．
故选C．
解：如图，设直线y=x+t与AB交于E，交BC于F，交OA于G，∵B（2，2）、C（1，4）、
∴直线BC的解析式为y=-2x+6，
依题意得
|
∴
|
∴FH=
| 6+2t |
| 3 |
| 2t |
| 3 |
∵直线y=x+t，∴∠AGE=45°，
∴当y=0时，x=t，
∴OG=t，
∴AG=2-t，
∴AE=2-t，BE=t，
∴S△EFB=
| 1 |
| 2 |
| 2t |
| 3 |
| 1 |
| 3 |
图象应该是抛物线的一部分，
所给四个答案只有C正确．
故选C．
点评：此题比较复杂，S与t（0≤t＜4）之间的函数分成三部分，由于第一部分是二次函数，图象是抛物线，由此即可判断选择项．
练习册系列答案
相关题目
如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，DE⊥EC，取DC的中点F，连接AF、BF．
ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．
如图，直角梯形ABCD中，AD∥BC，∠BCD=90°，且CD=2AD，tan∠ABC=2．
（2013•深圳二模）如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60°．以AD为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．
已知：如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，以AB为直径的⊙O切DC边于E点，AD=3cm，BC=5cm．求⊙O的面积．