题目内容
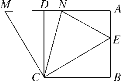
【题目】如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CE,CM.
(1)求证:∠BCE=∠DCM;
(2)若点N在边AD上,且∠NCE=45°,连接NC,NE,求证:NE=BE+DN;
(3)在(2)的条件下,若DN=2,MD=3,求正方形ABCD的边长.
【答案】(1)证明见解析;(2)证明见解析;(3)正方形ABCD的边长为6.
【解析】
(1)根据正方形的性质得到CD=BC,∠ADC=∠B=90°,
根据全等三角形的性质得到∠BCE=∠DCM;
(2)根据全等三角形的性质得到∠BCE=∠DCM,CE=CM,根据全等三角形的性质得到NE=MN,等量代换即可得到结论;
(3)设正方形的边长为x根据勾股定理即可得到结论.
(1)证明:在正方形ABCD中,
∵CD=BC,∠ADC=∠B=90°,
∴∠MDC=∠B=90°,
在△BCE与△CDM中,
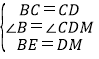 ,
,
∴△BCE≌△CDM,
∴∠BCE=∠DCM;
(2)∵∠NCE=45°,
∴∠BCE+∠DCN=45°,
∵△BCE≌△CDM,
∴∠BCE=∠DCM,CE=CM,
在△CEN与△CMN中,
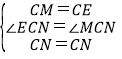 ,
,
∴△CEN≌△CMN,
∴NE=MN,
∵MN=MD+DN=BE+DN,
∴NE=BE+DN;
(3)设正方形的边长为x,
∵NE=BE+DN=MD+DN=3+2=5,AN=AD-DN=x-2,AE=x-3,
∵NE2=AN2+AE2,
∴52=(x-2)2+(x-3)2,
解得:x=6,或x=-1(不合题意,舍去),
∴正方形的边长是6.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目