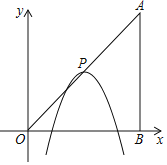题目内容
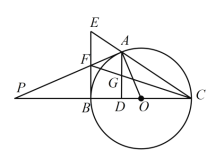
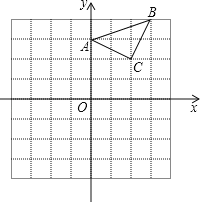
【题目】如图,已知一次函数y=ax+b(a,b为常数,a≠0)的图象与x轴,y轴分别交于点A,B,且与反比例函数y=![]() (k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于,若OA=OD=
(k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于,若OA=OD=![]() OB=3.
OB=3.
(1)求一次函数与反比例函数的解析式;
(2)观察图象直接写出不等式0<ax+b≤![]() 的解集.
的解集.

【答案】(1)![]() ,
,![]() ;(2)﹣3≤x<0
;(2)﹣3≤x<0
【解析】
(1)根据已知条件,结合平行线的性质得到CD=2OB=8,又因为OA=OD=![]() OB=3,可求得A(3,0),B(0,4),C(﹣3,8),再利用待定系数求一次函数与反比例函数的解析式即可;(2)根据C点的坐标为(﹣3,8),结合图象找到满足条件x的取值范围即可.
OB=3,可求得A(3,0),B(0,4),C(﹣3,8),再利用待定系数求一次函数与反比例函数的解析式即可;(2)根据C点的坐标为(﹣3,8),结合图象找到满足条件x的取值范围即可.
(1)∵CD⊥OA,
∴DC∥OB,
∴![]() ,
,
∴CD=2OB=8,
∵OA=OD=![]() OB=3,
OB=3,
∴A(3,0),B(0,4),C(﹣3,8),
把A、B两点的坐标分别代入y=ax+b可得![]() ,
,
解得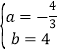 ,
,
∴一次函数解析式为![]() ,
,
∵反比例函数y=![]() 的图象经过点C,
的图象经过点C,
∴k=﹣24,
∴反比例函数的解析式为![]() ;
;
(2)由题意可知所求不等式的解集即为直线AC在x轴上方且在反比例函数图象下方的图象所对应的自变量的取值范围,即线段BC(包含C点,不包含B点)所对应的自变量x的取值范围,
∵C(﹣3,8),
∴0<﹣![]() x+4≤﹣
x+4≤﹣![]() 的解集为﹣3≤x<0.
的解集为﹣3≤x<0.

练习册系列答案
相关题目