ЬтФПФкШн
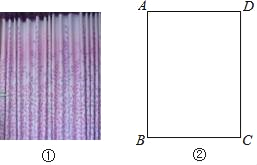
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDдкЦНУцжБНЧзјБъЯЕжаЃЌADЃН6ЃЌШєOAЁЂOBЕФГЄЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ7x+12ЃН0ЕФСНИіИљЃЌЧвOAЃОOBЃЎ
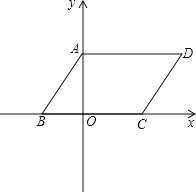
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ2ЃЉШєEЮЊxжсЩЯЕФЕуЃЌЧвSЁїAOEЃН![]() ЃЌЧѓОЙ§DЁЂEСНЕуЕФжБЯпЕФНтЮіЪНЃЌВЂХаЖЯЁїAOEгыЁїDAOЪЧЗёЯрЫЦЃП
ЃЌЧѓОЙ§DЁЂEСНЕуЕФжБЯпЕФНтЮіЪНЃЌВЂХаЖЯЁїAOEгыЁїDAOЪЧЗёЯрЫЦЃП
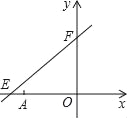
ЃЈ3ЃЉШєЕуMдкЦНУцжБНЧзјБъЯЕФкЃЌдђдкжБЯпABЩЯЪЧЗёДцдкЕуFЃЌЪЙвдAЁЂCЁЂFЁЂMЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃПШєДцдкЃЌЧыжБНгаДГіFЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉyЃН
ЃЛЃЈ2ЃЉyЃН![]() xЉ
xЉ![]() ЛђyЃН
ЛђyЃН![]() x+
x+![]() ЃЌЁїAOEЁзЁїDAOЃЛЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕугаЫФИіЃКF1ЃЈЉ3ЃЌ0ЃЉЃЛF2ЃЈ3ЃЌ8ЃЉЃЛF3ЃЈЉ
ЃЌЁїAOEЁзЁїDAOЃЛЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕугаЫФИіЃКF1ЃЈЉ3ЃЌ0ЃЉЃЛF2ЃЈ3ЃЌ8ЃЉЃЛF3ЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛF4ЃЈЉ
ЃЉЃЛF4ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНтвЛдЊЖўДЮЗНГЬЧѓГіOAЃЌOBЕФГЄЖШЃЌдйРћгУЙДЙЩЖЈРэЧѓГіABЕФГЄЖШЃЌдйДњШыМЦЫуМДПЩЃЛ
ЃЈ2ЃЉЯШИљОнШ§НЧаЮЕФУцЛ§ЧѓГіЕуEЕФзјБъЃЌВЂИљОнЦНааЫФБпаЮЕФЖдБпЯрЕШЕФаджЪЧѓГіЕуDЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтжБЯпЕФНтЮіЪНЃЛЗжБ№ЧѓГіСНШ§НЧаЮМажБНЧЕФСНЖдгІБпЕФБШЃЌШчЙћЯрЕШЃЌдђСНШ§НЧаЮЯрЫЦЃЌЗёдђВЛЯрЫЦЃЛ
ЃЈ3ЃЉИљОнСтаЮЕФаджЪЃЌЗжACгыAFЪЧСкБпВЂЧвЕуFдкЩфЯпABЩЯгыЩфЯпBAЩЯСНжжЧщПіЃЌвдМАACгыAFЗжБ№ЪЧЖдНЧЯпЕФЧщПіЗжБ№НјааЧѓНтМЦЫуЃЎ
НтЃКЃЈ1ЃЉx2Љ7x+12ЃН0ЃЌ
ЃЈxЉ3ЃЉЃЈxЉ4ЃЉЃН0ЃЌ
ЁрxЉ3ЃН0ЃЌxЉ4ЃН0ЃЌ
НтЕУx1ЃН3ЃЌx2ЃН4ЃЌ
ЁпOAЃОOBЃЌ
ЁрOAЃН4ЃЌOBЃН3ЃЌ
дкЁїAOBжаЃЌABЃН![]() ЃН
ЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁрsinЁЯABCЃН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉИљОнЬтвтЃЌЩшEЃЈxЃЌ0ЃЉЃЌдђ
SЁїAOEЃН![]() ЁСOAЁСxЃН
ЁСOAЁСxЃН![]() ЁС4xЃН
ЁС4xЃН![]() ЃЌ
ЃЌ
НтЕУxЃН![]() ЃЌ
ЃЌ
ЁрEЃЈ![]() ЃЌ0ЃЉЛђЃЈЉ
ЃЌ0ЃЉЛђЃЈЉ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌ
ЁрЕуDЕФзјБъЪЧЃЈ6ЃЌ4ЃЉЃЌ
ЩшОЙ§DЁЂEСНЕуЕФжБЯпЕФНтЮіЪНЮЊyЃНkx+bЃЌ
дђЂй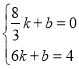 ЃЌ
ЃЌ
НтЕУ 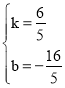 ЃЌ
ЃЌ
ЁрНтЮіЪНЮЊyЃН![]() xЉ
xЉ![]() ЃЛ
ЃЛ
Ђк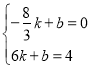 ЃЌ
ЃЌ
НтЕУ ЃЌ
ЃЌ
НтЮіЪНЮЊЃК yЃН![]() x+
x+![]()
дкЁїAOEгыЁїDAOжаЃЌ ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁпЁЯAOEЃНЁЯOADЃН90ЁуЃЌ
ЁрЁїAOEЁзЁїDAOЃЛ
ЃЈ3ЃЉИљОнМЦЫуЕФЪ§ОнЃЌOBЃНOCЃН3ЃЌ
ЁрAOЦНЗжЁЯBACЃЌ
ЂйACЁЂAFЪЧСкБпЃЌЕуFдкЩфЯпABЩЯЪБЃЌAFЃНACЃН5ЃЌ
ЫљвдЕуFгыBжиКЯЃЌ
МДFЃЈЉ3ЃЌ0ЃЉЃЌ
ЂкACЁЂAFЪЧСкБпЃЌЕуFдкЩфЯпBAЩЯЪБЃЌMгІдкжБЯпADЩЯЃЌЧвFCДЙжБЦНЗжAMЃЌ
ЕуFЃЈ3ЃЌ8ЃЉЃЎ
ЂлACЪЧЖдНЧЯпЪБЃЌзіACДЙжБЦНЗжЯпLЃЌACНтЮіЪНЮЊyЃНЉ![]() x+4ЃЌжБЯпLЙ§ЃЈ
x+4ЃЌжБЯпLЙ§ЃЈ![]() ЃЌ2ЃЉЃЌЧвkжЕЮЊ
ЃЌ2ЃЉЃЌЧвkжЕЮЊ![]() ЃЈЦНУцФкЛЅЯрДЙжБЕФСНЬѕжБЯпkжЕГЫЛ§ЮЊЉ1ЃЉЃЌ
ЃЈЦНУцФкЛЅЯрДЙжБЕФСНЬѕжБЯпkжЕГЫЛ§ЮЊЉ1ЃЉЃЌ
LНтЮіЪНЮЊyЃН![]() x+
x+![]() ЃЌСЊСЂжБЯпLгыжБЯпABЧѓНЛЕуЃЌ
ЃЌСЊСЂжБЯпLгыжБЯпABЧѓНЛЕуЃЌ
ЁрFЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЂмAFЪЧЖдНЧЯпЪБЃЌЙ§CзіABДЙЯпЃЌДЙзуЮЊNЃЌИљОнЕШЛ§ЗЈЧѓГіCNЃН![]() ЃЌЙДЙЩЖЈРэЕУГіЃЌANЃН
ЃЌЙДЙЩЖЈРэЕУГіЃЌANЃН![]() ЃЌзіAЙигкNЕФЖдГЦЕуМДЮЊFЃЌAFЃН
ЃЌзіAЙигкNЕФЖдГЦЕуМДЮЊFЃЌAFЃН![]() ЃЌЙ§FзіyжсДЙЯпЃЌДЙзуЮЊGЃЌFGЃН
ЃЌЙ§FзіyжсДЙЯпЃЌДЙзуЮЊGЃЌFGЃН![]() ЃЌ
ЃЌ
ЁрFЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕугаЫФИіЃКF1ЃЈЉ3ЃЌ0ЃЉЃЛF2ЃЈ3ЃЌ8ЃЉЃЛF3ЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛF4ЃЈЉ
ЃЉЃЛF4ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ


ЁОЬтФПЁПНЋЕШбќRtЁїABCШЦЕуAФцЪБеыа§зЊ15ЁуЕУЕНЁїABЁфCЁфЃЌШєAC=1ЃЌдђЭМжавѕгАВПЗжУцЛ§ЮЊЃЈЁЁЁЁЃЉ
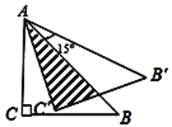
A.![]() B.3
B.3![]() C.
C.![]() D.
D.![]()
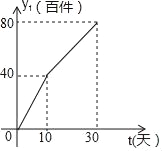
ЁОЬтФПЁПЮвЪаКьСьЗўЪЮгаЯоЙЋЫОЩњВњСЫвЛПюЯФМОЗўзАЃЌЭЈЙ§ЪЕбщЩЬЕъКЭЭјЩЯЩЬЕъСНжжЭООЖНјааЯњЪлЃЌЯњЪлвЛЖЮЪБМфКѓЃЌИУЙЋЫОЖдетжжЩЬЦЗЕФЯњЪлЧщПіЃЌНјааСЫЮЊЦк30ЬьЕФИњзйЕїВщЃЌЦфжаЪЕЬхЩЬЕъЕФШеЯњЪлСПy1ЃЈАйМўЃЉгыЪБМфtЃЈtЮЊећЪ§ЃЌЕЅЮЛЃКЬьЃЉЕФВПЗжЖдгІжЕШчБэЫљЪОЃК
ЪБМфtЃЈЬьЃЉ | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
ШеЯњЪлСПytЃЈАйМўЃЉ | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
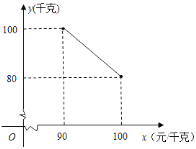
ЃЈ1ЃЉЧыФудквЛДЮКЏЪ§ЁЂЖўДЮКЏЪ§КЭЗДБШР§КЏЪ§жаЃЌбЁдёКЯЪЪЕФКЏЪ§ФмЗДгГy1гыtЕФБфЛЏЙцТЩЃЌВЂЧѓГіy1гыtЕФКЏЪ§ЙиЯЕЪНМАздБфСПtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЭјЩЯЩЬЕъЕФШеЯњЪлСПy2ЃЈАйМўЃЉгыЪБМфtЃЈtЮЊећЪ§ЃЌЕЅЮЛЃКЬьЃЉЕФЙиЯЕШчЭМЫљЪОЃЎЧѓy2гыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкИњзйЕїВщЕФ30ЬьжаЃЌЩшЪЕЬхЩЬЕъКЭЭјЩЯЩЬЕъЕФШеЯњЪлзмСПЮЊyЃЈАйМўЃЉЃЌЧѓyгыtЕФКЏЪ§ЙиЯЕЪНЃЛЕБtЮЊКЮжЕЪБЃЌШеЯњЪлзмСПyДяЕНзюДѓЃЌВЂЧѓГіДЫЪБЕФзюДѓжЕЃЎ