题目内容
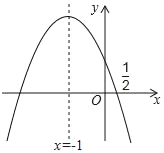
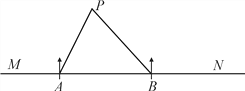
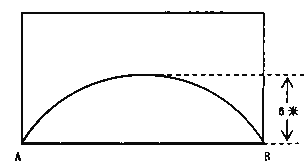
【题目】为了实现省城合肥跨越发展,近两年我市开始全面实施“畅通一环”工程,如图为一环路的一座下穿路拱桥,它轮廓是抛物线,桥的跨度AB=16米,拱高为6米.
(1)请以A点为坐标原点,AB所在直线为x轴建立平面直角坐标系,将抛物线放在直角坐标系中,求出抛物线的解析式;
(2)若桥拱下是双向行车道,其中一条行车道能否并排行驶宽3米,高2米的两辆汽车(汽车间隔不小于1米)说明理由
【答案】(1)建图见解析;y=![]() .(0≤x≤16);(2)不能,理由见解析.
.(0≤x≤16);(2)不能,理由见解析.
【解析】
(1)根据题目可知A、B,C的坐标,设出抛物线的解析式代入可求解;
(2)设DE是两辆车的宽度和,作EG垂直AB交抛物线于G,求出EG则可求解.
解:(1)以A点为坐标原点,AB所在直线为x轴建立平面直角坐标系,如图:
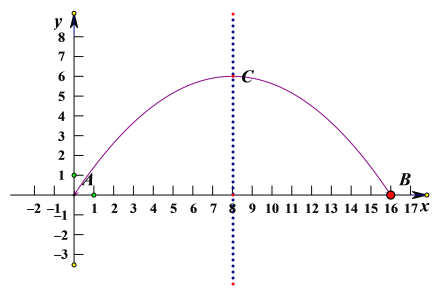
根据题目条件,A、B的坐标分别是(0,0)、(16,0)、顶点C的坐标是(8,6).
设抛物线的解析式y=a(x-8)2+6,将A的坐标代入得64a+6=0,
解得:a=![]() .
.
所以抛物线的表达式是y=![]() ;(0≤x≤16);
;(0≤x≤16);
(2)设DE是两辆车最内侧与最外侧的宽度和=3+1+3=7,AE=1,则E点坐标是(1,0),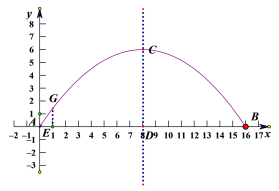
过E点作EG垂直AB交抛物线于G,则yH=![]() =
=![]() <2,
<2,
根据抛物线的特点,可知一条行车道不能并排行驶宽3米,高2米的两辆汽车(汽车间隔不小于1米).

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目