题目内容
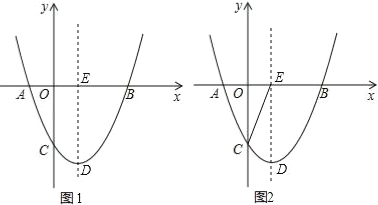
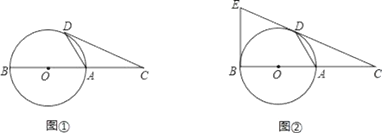
【题目】已知点C为直径BA的延长线上一点,CD切⊙O于点D,
(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
【答案】(I)∠DAB =64°;(II) BE的长是![]()
【解析】
(I)根据切线的性质得出∠ODC=90°,求出∠ODA,根据等腰三角形的性质求出即可;
(II)根据切线长定理得出BE=DE,根据勾股定理求出DC,根据勾股定理得出方程,求出方程的解即可.
(I)如图①,连接OD,
∵CD切⊙O于点D,
∴∠ODC=90°,
∴∠CDA+∠ODA=90°,
∵∠CDA=26°,
∴∠ADO=64°,
∵OD=OA,
∴∠DAB=∠ODA=64°;
(II)如图②,连接OD,
在Rt△ODC中,OC=BCOB=103=7,
![]()
∵ED、EB分别为⊙O的切线,
∴ED=EB,
在Rt△CBE中,设BE=x,由![]() 得:
得:![]()
解得:![]()
∴BE的长是![]()


练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目