题目内容
【题目】如图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120),已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1)当速度为50km/h、100km/h时,该汽车的耗油量分别为 L/km、 L/km.
(2)求线段AB所表示的y与x之间的函数表达式.
(3)速度是多少时,该汽车的耗油量最低.最低是多少.
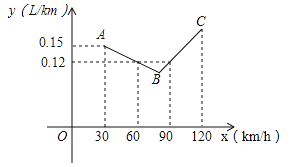
【答案】(1)0.13,0.14;(2)y=﹣0.001x+0.18;(3)速度是80km/h时,该汽车的耗油量最低,最低是0.1L/km.
【解析】
(1)和(2):先求线段AB的解析式,因为速度为50km/h的点 在AB上,所以将x=50代入计算即可,速度是100km/h的点在线段BC上,可由已知中的“该汽车的速度每增加1km/h,耗油量增加0,002L/km”列式求得,也可以利用解析式求解;
(3)观察图形发现,两线段的交点即为最低点,因此求两函数解析式组成的方程组的解即可.
解:(1)设AB的解析式为:y=kx+b,
把(30,0.15)和(60,0.12)代入y=kx+b中得:
![]() ,解得
,解得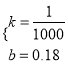 ,
,
∴AB:y=-0.001x+0.18,
当x=50时,y=-0.001×50+0.18=0.13,
由线段BC上一点坐标(90,0.12)得:0.12+(100-90)×0.002=0.14,
故答案为0.13,0.14;
(2)设线段AB 所表示的y 与x 之间的函数表达式为y=kx+b.
因为y=kx+b 的图像过点(30,0.15)与(60,0.12),所以![]()
解方程组,得k=-0.001,b=0.18.
所以线段AB 所表示的y 与x 之间的函数表达式为y=-0.001x+0.18.
(3)根据题意,得线段BC 所表示的y 与x 之间的函数表达式为y=0.12+0.002(x-90)
=0.002x-0.06.
由图像可知,B 是折线ABC 的最低点.
解方程组![]() ,得
,得![]()
因此,速度是80 km/h 时,该汽车的耗油量最低,最低是0.1 L / km.