题目内容
【题目】如图,已知点C、D在线段AB上,且AC=4,BD=9,△PCD是边长为6的等边三角形.
(1)求证:△PAC∽△BPD;
(2)求∠APB的度数.
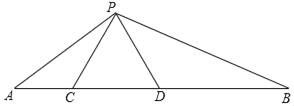
【答案】(1)见解析;(2)120°.
【解析】
试题(1)根据等边三角形的性质得到PC=CD=PD=6,∠PCD=∠PDC=60°,得出∠ACP=∠PDB=120°,由AC=4,BD=9,AC:PD=PC:BD,即可证出△ACP∽△PDB;
(2)由相似三角形的对应角相等,得出∠APC=∠PBD,由三角形内角和定理得出∠DPB+∠DBP=60°,即∠APC+∠BPD=60°,可求出∠APB=120°.
试题解析:(1)∵等边△PCD的边长为6,
∴PC=PD=6,∠PCD=∠PDC=60°,
又∵AC=4,BD=9,
∴![]() ,
,
∵等边△PCD中,∠PCD=∠PDC=60°,
∴∠PCA=∠PDB=120°,
∴△ACP∽△PDB;
(2)∵△ACP∽△PDB,
∴∠APC=∠PBD,
∵∠PDB=120°,
∴∠DPB+∠DBP=60°,
∴∠APC+∠BPD=60°,
∴∠APB=∠CPD+∠APC+∠BPD=120°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目