题目内容
如图,在四边形ABCD中,AC=BD,且AC⊥BD, E、F、G、H分别是AB、BC、CD、DA的中点.则四边形EFGH是怎样的四边形?证明你的结论.


四边形EFGH是正方形 证明见解析
试题分析:先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.
试题解析:在△ABC中,E、F分别是AB、BC的中点,
故可得:EF=
 AC,同理FG=
AC,同理FG= BD,GH=
BD,GH= AC,HE=
AC,HE= BD,
BD,在梯形ABCD中,AB=DC,
故AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.

练习册系列答案
相关题目


 的外角,则
的外角,则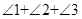 =
=