题目内容
【题目】如图,AD是⊙O的直径,以A为圆心,弦AB为半径画弧交⊙O于点C,连结BC交AD于点E,若DE=3,BC=8,则⊙O的半径长为( )

A.![]() B.5C.
B.5C.![]() D.
D.![]()
【答案】A
【解析】
由作法得![]() ,根据圆周角定理得到∠ADB=∠ABE,再根据垂径定理的推论得到AD⊥BC,BE=CE=
,根据圆周角定理得到∠ADB=∠ABE,再根据垂径定理的推论得到AD⊥BC,BE=CE=![]() BC=4,于是可判断Rt△ABE∽Rt△BDE,然后利用相似比求出AE,从而得到圆的直径和半径.
BC=4,于是可判断Rt△ABE∽Rt△BDE,然后利用相似比求出AE,从而得到圆的直径和半径.
解:由作法得AC=AB,
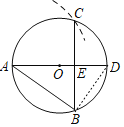
∴![]() ,
,
∴∠ADB=∠ABE,
∵AB为直径,
∴AD⊥BC,
∴BE=CE=![]() BC=4,∠BEA=∠BED=90°,
BC=4,∠BEA=∠BED=90°,
而∠BDE=∠ABE,
∴Rt△ABE∽Rt△BDE,
∴BE:DE=AE:BE,即4:3=AE:4,
∴AE=![]() ,
,
∴AD=AE+DE=![]() +3=
+3=![]() ,
,
∴⊙O的半径长为![]() .
.
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目