题目内容
【题目】在平面直角坐标系![]() 中,如图所示,已知
中,如图所示,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,在
轴上,在![]() 中,点
中,点![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() .
.![]() ,
,![]() ,
,![]() .按下列要求画图(保留作图痕迹):
.按下列要求画图(保留作图痕迹):
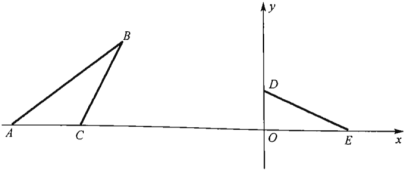
(1)将![]() 绕
绕![]() 点按逆时针方向旋转90°得到
点按逆时针方向旋转90°得到![]() (其中点
(其中点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ),画出
),画出![]() .
.
(2)将![]() 沿
沿![]() 轴向右平移得到
轴向右平移得到![]() (其中点
(其中点![]() ,
,![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() ),使得边
),使得边![]() 与(1)中的
与(1)中的![]() 的边
的边![]() 重合.
重合.
(3)求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)6
【解析】
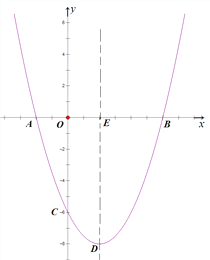
(1)以点O为圆心,以OE为半径画弧,与y轴正半轴相交于点N,以OD为半径画弧,与x轴负半轴相交于点M,连接MN即可;
(2)以M为圆心,以AC长为半径画弧与x轴负半轴相交于点A',B'与N重合,C'与M重合,然后顺次连接即可;
(3)设OE=x,则ON=x,作MF⊥A'B'于点F,判断出B'C'平分∠A'B'O,再根据全等三角形的性质可得B'F=B'O=OE=x,FC'=OC'=OD=3,利用勾股定理列式求出A'F,然后表示出A'B'、A'O.在Rt△A'B'O中,利用勾股定理列出方程求解即可.
(1)△OMN如图所示;
(2)△A'B'C'如图所示;
(3)设OE=x,则ON=x,作MF⊥A'B'于点F,
由作图可知:B'C'平分∠A'B'O,且C'O⊥OB',
∴∠B'FM=∠MON=90°,∠FB'M=∠OB'M.
∵B'M=B'M,
∴△FB'M≌△OB'M,
∴B'F=B'O=OE=x,FC'=OC'=OD=3.
∵A'C'=AC=5,
∴A'F![]() 4,
4,
∴A'B'=x+4,A'O=5+3=8,
在Rt△A'B'O中,x2+82=(4+x)2,
解得:x=6,
即OE=6.

【题目】学校冬季趣味运动会开设了“抢收抢种”项目,八(5)班甲、乙两个小组都想代表班级参赛,为了选择一个比较好的队伍,八(5)班的班委组织了一次选拔赛,甲、乙两组各10人的比赛成绩如下表:
甲组 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙组 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲组成绩的中位数是 分,乙组成绩的众数是 分.
(2)计算乙组的平均成绩和方差.
(3)已知甲组成绩的方差是1.4,则选择 组代表八(5)班参加学校比赛.