题目内容
【题目】如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为 ． 
【答案】2 
或4﹣2
【解析】解：如图，当直线l在直线CE上方时，连接DE交直线l于M，
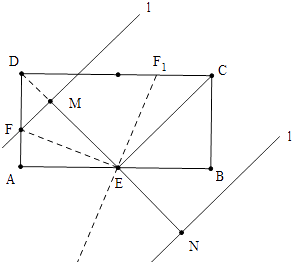
∵四边形ABCD是矩形，
∴∠A=∠B=90°，AD=BC，
∵AB=4，AD=BC=2，
∴AD=AE=EB=BC=2，
∴△ADE、△ECB是等腰直角三角形，
∴∠AED=∠BEC=45°，
∴∠DEC=90°，
∵l∥EC，
∴ED⊥l，
∴EM=2=AE，
∴点A、点M关于直线EF对称，
∵∠MDF=∠MFD=45°，
∴DM=MF=DE﹣EM=2 ﹣2，
∴DF= DM=4﹣2 ．
当直线l在直线EC下方时，
∵∠DEF1=∠BEF1=∠DF1E，
∴DF1=DE=2 ，
综上所述DF的长为2 或4﹣2 ．
所以答案是2 或4﹣2 ．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
相关题目
【题目】某工厂计划生产A、B两种产品共10件，其生产成本和利润如下表．
A种产品 | B种产品 | |
成本（万元/件） | 2 | 5 |
利润（万元/件） | 1 | 3 |
（1）若工厂计划获利14万元，问A，B两种产品应分别生产多少件？
（2）若工厂计划投入资金不多于44万元，且获利多于14万元，求工厂的最大利润？
