题目内容
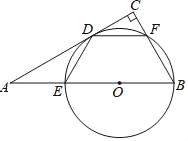
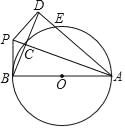
【题目】如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
【答案】(1)PB与⊙O相切,理由见解析;(2)⊙O的半径为4.5.
【解析】
(1)根据线段垂直平分线的性质可得PB=PD,通过证明△ABP与△ADP全等,根据全等三角形对应角相等可得∠ABP=∠ADP=90°,再根据切线的判定定理即可得证;
(2)根据全等三角形的性质得∠BAC=∠DAC,得到BC=CE=3,然后证明△DCE与△DAB相似,然后根据相似三角形的对应边成比可推导得出DCDB=DEDA,代入相关数据即可求得答案.
(1)PB与⊙O相切,理由如下:
∵AB是⊙O的直径,
∴AC⊥BD,
又AB=AD,
∴AP是线段BD的垂直平分线,
∴PB=PD,
在△ABP和△ADP中,
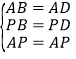 ,
,
∴△ABP≌△ADP(SSS),
∴∠ABP=∠ADP=90°,
∴PB与⊙O相切;
(2)∵△ABP≌△ADP,
∴∠BAC=∠DAC,
∴![]() ,
,
∴BC=CE=3,
∵AB=AD,AC⊥BD,
∴BC=CD=3,
∵四边形ABCE是⊙O的内接四边形,
∴∠DBA+∠CEA=180°,
∵∠DEC+∠CEA=180°,
∴∠DBA=∠DEC,
又∵∠CDE=∠ADB,
∴△DCE∽△DAB,
∴DC:DA=DE:DB,
∴DCDB=DEDA,即3×6=DE×(DE+7),
解得,DE=2,
∴DA=2+7=9,
∴AB=AD=9,
∴⊙O的半径为4.5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目