Question

【题目】如图1，四边形ABCD为矩形，曲线L经过点D．点Q是四边形ABCD内一定点，点P是线段AB上一动点，作PM⊥AB交曲线L于点M，连接QM．

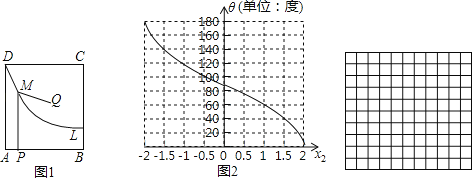
小东同学发现：在点P由A运动到B的过程中，对于x1＝AP的每一个确定的值，θ＝∠QMP都有唯一确定的值与其对应，x1与θ的对应关系如表所示：

x1＝AP	0	1	2	3	4	5
θ＝∠QMP	α	85°	130°	180°	145°	130°

小芸同学在读书时，发现了另外一个函数：对于自变量x2在﹣2≤x2≤2范围内的每一个值，都有唯一确定的角度θ与之对应，x2与θ的对应关系如图2所示：

根据以上材料，回答问题：

（1）表格中α的值为　 　．

（2）如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等，可以在两个变量x1与x2之间建立函数关系．

①在这个函数关系中，自变量是　 ，因变量是　 ；（分别填入x1和x2）

②请在网格中建立平面直角坐标系，并画出这个函数的图象；

③根据画出的函数图象，当AP＝3.5时，x2的值约为　 ．

Answer 1

【答案】（1）50°；（2）①x1，x2；②见解析；③﹣1.87（答案不唯一）．

【解析】

（1）x=0时和x=5时，两个θ角为同旁内角，即可求解；
（2）①根据变量的定义即可求解；
②根据表格中θ的数据，从图2读出θ对应的x2的数据并列表，依据表格数据描图即可；
③当AP=3.5时，即x1=3.5时，从图象读出x2的值即可．

（1）当x＝5时，θ＝∠QMP＝130°，当x＝0时，θ＝∠QMP＝α，

x＝0时和x＝5时，两个θ角为AD∥BC时的两个同旁内角，故α＝180°﹣130°＝50°，

故答案为50°；

（2）①根据变量的定义，x1是自变量，x2是因变量；

故答案为：x1，x2；

②根据表格中θ的数据，从图2读出θ对应的x2的数据并列出下表：

依据上述表格数据，描点绘出下图：

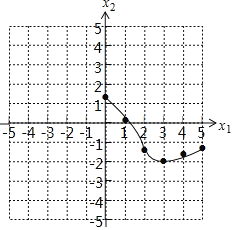
③当AP＝3.5时，即x1＝3.5时，从图象看x2的值约为﹣1.87，

故答案为﹣1.87（答案不唯一）．