题目内容
【题目】如图，在△ABC中，AB=AC，AD平分∠BAC． 求证：△ABD≌△ACD．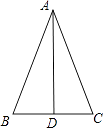
【答案】证明：∵AD平分∠BAC， ∴∠BAD=∠CAD，
在△ABD和△ACD中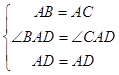
，
∴△ABD≌△ACD．
【解析】根据角平分线的定义得出∠BAD=∠CAD，根据SAS即可证出答案．
【考点精析】利用三角形的“三线”和等腰三角形的性质对题目进行判断即可得到答案，需要熟知1、三角形角平分线的三条角平分线交于一点(交点在三角形内部，是三角形内切圆的圆心，称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部，是三角形的几何中心，称为中心);3、三角形的高线是顶点到对边的距离；注意：三角形的中线和角平分线都在三角形内；等腰三角形的两个底角相等（简称：等边对等角）．
练习册系列答案
相关题目
