题目内容
【题目】对于平面直角坐标系xOy中的点P,给出如下定义:记点P到x轴的距离为![]() ,到y轴的距离为
,到y轴的距离为![]() ,若
,若![]() ,则称
,则称![]() 为点P的最大距离;若
为点P的最大距离;若![]() ,则称
,则称![]() 为点P的最大距离.
为点P的最大距离.
例如:点P(![]() ,
,![]() )到到x轴的距离为4,到y轴的距离为3,因为3 < 4,所以点P的最大距离为
)到到x轴的距离为4,到y轴的距离为3,因为3 < 4,所以点P的最大距离为![]() .
.
(1)①点A(2,![]() )的最大距离为 ;
)的最大距离为 ;
②若点B(![]() ,
,![]() )的最大距离为
)的最大距离为![]() ,则
,则![]() 的值为 ;
的值为 ;
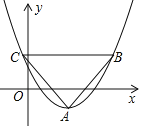
(2)若点C在直线![]() 上,且点C的最大距离为
上,且点C的最大距离为![]() ,求点C的坐标;
,求点C的坐标;

(3)若⊙O上存在点M,使点M的最大距离为![]() ,直接写出⊙O的半径r的取值范围.
,直接写出⊙O的半径r的取值范围.
【答案】(1)①5; ②![]() ;(2)C(
;(2)C(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)
);(3) ![]() .
.
【解析】
(1)①直接根据“最大距离”的定义,其最小距离为“最大距离”;
②点B(a,2)到x轴的距离为2,且其“最大距离”为5,所以a=±5;
(2)根据点C的“最大距离”为5,可得x=±5或y=±5,代入可得结果;
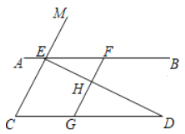
(3)如图,观察图象可知:当⊙O于直线x=5,直线x=-5,直线y=5,直线y=-5有交点时,⊙O上存在点M,使点M的最大距离为5,
(1)①∵点A(2,-5)到x轴的距离为5,到y轴的距离为2,
∵2<5,
∴点A的“最大距离”为5.
②∵点B(a,2)的“最大距离”为5,
∴a=±5;
故答案为5,±5.
(2)设点C的坐标(x,y),
∵点C的“最大距离”为5,
∴x=±5或y=±5,
当x=5时,y=-7,
当x=-5时,y=3,
当y=5时,x=-7,
当y=-5时,x=3,
∴点C(-5,3)或(3,-5).
(3)如图,观察图象可知:当⊙O于直线x=5,直线x=-5,直线y=5,直线y=-5有交点时,⊙O上存在点M,使点M的最大距离为5,
∴5≤r≤5![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校在“清明节”前组织七年级全体学生进行了一次“缅怀先烈,牢记历史”知识竞赛,赛后随机抽取了部分学生成绩进行统计,制作如下频数分布表和频数分布直方图,请根据图中提供的信息,解答下列问题:
分数段 | 频数 | 频率 |
| 4 |
|
| 8 | b |
| a |
|
| 10 |
|
| 6 |
|
![]() 表中
表中![]() ______,
______,![]() ______,并补全直方图;
______,并补全直方图;
![]() 若用扇形统计图描述次成绩统计图分别情况,则分数段
若用扇形统计图描述次成绩统计图分别情况,则分数段![]() 对应扇形的圆心角度数是______;
对应扇形的圆心角度数是______;
![]() 若该校七年级共900名学生,请估计该年级分数在
若该校七年级共900名学生,请估计该年级分数在![]() 的学生有多少人?
的学生有多少人?