题目内容
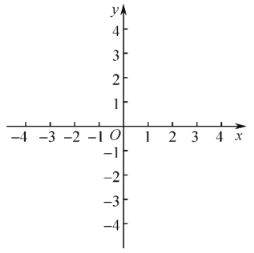
【题目】在平面直角坐标系![]() 中,抛物线
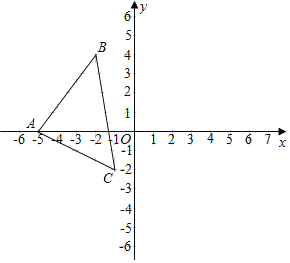
中,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点B的坐标为
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点B的坐标为![]() ,将直线
,将直线![]() 沿y轴向上平移3个单位长度后,恰好经过B、C两点.
沿y轴向上平移3个单位长度后,恰好经过B、C两点.
(1)求k的值和点C的坐标;
(2)求抛物线![]() 的表达式及顶点D的坐标;
的表达式及顶点D的坐标;
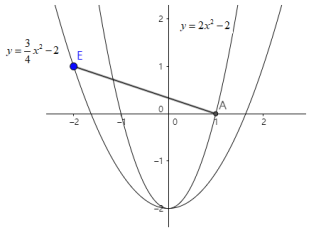
(3)已知点E是点D关于原点的对称点,若抛物线![]() 与线段
与线段![]() 恰有一个公共点,结合函数的图象,求a的取值范围.
恰有一个公共点,结合函数的图象,求a的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)将直线![]() 沿y轴向上平移3个单位长度后得到
沿y轴向上平移3个单位长度后得到![]() ,并且经过点
,并且经过点![]() ,代入求得
,代入求得![]() 值,且C点为抛物线
值,且C点为抛物线![]() 与y轴交点,则C点坐标为
与y轴交点,则C点坐标为![]() ,
,![]() 也经过C点,代入可求出C点坐标;
也经过C点,代入可求出C点坐标;
(2)已知B、C两点的坐标,根据待定系数法即可求出抛物线![]() 的解析式,再根据顶点式则可求出顶点坐标;
的解析式,再根据顶点式则可求出顶点坐标;
(3)将A、E两点的坐标分别代入抛物线![]() 的解析式即可求出相应的
的解析式即可求出相应的![]() 值,通过观察图象,上下移动图象即可求出抛物线
值,通过观察图象,上下移动图象即可求出抛物线![]() 与线段AE有一个公共点时
与线段AE有一个公共点时![]() 的范围.
的范围.
(1)解:将直线![]() 沿y轴向上平移3个单位长度后得到
沿y轴向上平移3个单位长度后得到![]() ,
,
∵直线![]() 经过点
经过点![]() ,
,
∴![]() ,
,
则![]() .
.
C点为抛物线![]() 与y轴交点,则C点坐标为
与y轴交点,则C点坐标为![]() ,
,
且![]() 经过点
经过点![]() ,代入得:
,代入得:![]() ,则C点坐标为
,则C点坐标为![]() .
.
(2)解:抛物线![]() 经过点
经过点![]() 和点
和点![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴抛物线![]() 的函数表达式为
的函数表达式为![]() ,
,
∴![]() ,
,
∴顶点D的坐标为![]() .
.
(3)解:∵点E是点D关于原点的对称点,
∴点E的坐标为![]() .
.
当![]() 经过点
经过点![]() 时,
时,![]() ,则
,则![]() ,
,
当![]() 经过点
经过点![]() 时,
时,![]() ,则
,则![]() ,
,
结合下面图象可知a的取值范围是![]() .
.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
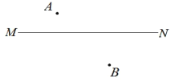
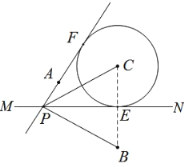
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.