题目内容
【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,连接CO,过B作BD//OC交⊙O于D,连接AD交OC于G,延长AB、CD交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=4,DE=8,
①求CD的长;
②连接BC交AD于F,求![]() 的值.
的值.

【答案】(1)见解析;(2)①CD=12;②![]() .
.
【解析】
(1)连接OD,由直径所对的圆周角为直角及切线的性质,可得∠CAB=90°=∠ADB,从而可判定△AOC≌△DOC(SAS),由全等三角形的性质可得∠CDO=90°,从而由切线的判定定理可得答案;
(2)①设⊙O的半径为r,则OD=OB=r,由勾股定理解得r,再由平行线截线段成比例定理可得比例式,从而求得CD的长;
②由CO∥BD,可判定△BDF∽△CGF;△EBD∽△EOC,从而可得比例式,结合相似三角形的性质可得答案.
(1)证明:如图,连接OD,
∵AB为⊙O的直径,AC为⊙O的切线,
∴∠CAB=90°=∠ADB,
∵OD=OB,
∴∠DBO=∠BDO,
∴CO//BD,
![]()
∴∠AOC=∠COD,且AO=OD,CO=CO,
∴△AOC≌△DOC(SAS),
∴∠CAO=∠CDO=90°,
∴OD⊥CD,且OD是半径,
∴CD是⊙O的切线;
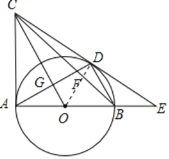
(2)①设⊙O的半径为r,则OD=OB=r,
在Rt△ODE中,
∵![]()
∴![]() ,
,
解得r=6,
∴OB=6,
∵CO//BD,
∴![]() ,
,
∴CD=12;
②∵CO//BD,
∴△BDF∽△CGF;△EBD∽△EOC.
∴![]()
设OG=x,
∵OG为△ABD的中位线,
∴BD=2OG=2x,
![]() BE=4,
BE=4,![]()
![]() OE=10,
OE=10,
∴OC=5x,CG=4x,
∴![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目