题目内容
【题目】如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在 ![]() 上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
A.![]()
![]()
B.![]()
![]()
C.2﹣ ![]()
![]()
D.2 ![]() ﹣2
﹣2
【答案】B
【解析】解:如图延长AN交y轴于Q1 , 延长AM交y轴于Q2 , 作NE⊥OA于E,
∵M、N是半圆的三等分点,
∴∠NBO=∠MBN=∠MBA=60°,
在RT△BNE中,∵BN=1,∠NBE=60°,
∴∠BNE=30°,EB= ![]() BN=
BN= ![]() ,NE=
,NE= ![]() EB=
EB= ![]() ,
,
∵NE∥OQ1 ,
∴ ![]() ,
,
∴ ![]() ,
,
∴OQ1= ![]() ,
,
∵BM=BG,∠MBG=60°,
∴△MBG是等边三角形,
∴MG=BM=AG,
∴∠AMB=90°,∠MAB=30°,
在RT△AOQ2中,∵AO=4,∠OAQ2=30°,
∴OQ2= ![]() OA=
OA= ![]() ,
,
∴Q1Q2=OQ2﹣OQ1= ![]() .
.
故选B.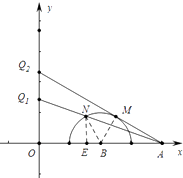
【考点精析】根据题目的已知条件,利用圆心角、弧、弦的关系和切线的性质定理的相关知识可以得到问题的答案,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目