题目内容
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证: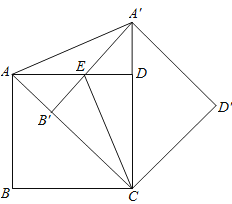
(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠A′DE=90°,
根据旋转的方法可得:∠EA′D=45°,
∴∠A′ED=45°,
∴A′D=DE,
在△AA′D和△CED中
AD=CD
∠ADA′=∠EDC
A′D=ED∴△AA′D≌△CED(SAS);
(2)
证明:∵根据旋转可得AC=A′C,
∴点C在AA′的垂直平分线上,
∵AC是正方形ABCD的对角线,
∴∠CAE=45°,
∵AC=A′C,CD=CB′,
∴AB′=A′D,
在△AEB′和△A′ED中
∠EAB′=∠EA′D
∠AEB′=∠A′ED
AB′=A′D
∴△AEB′≌△A′ED,
∴AE=A′E,
∴点E也在AA′的垂直平分线上,
∴直线CE是线段AA′的垂直平分线
【解析】(1)根据正方形的性质可得AD=CD,∠ADC=90°,∠EA′D=45°,则∠A′DE=90°,再计算出∠A′ED=45°,根据等角对等边可得A′D=ED,即可利用SAS证明△AA′D≌△CED;(2)首先由AC=A′C,可得点C在AA′的垂直平分线上;再证明△AEB′≌△A′ED,可得AE=A′E,进而得到点E也在AA′的垂直平分线上,再根据两点确定一条直线可得直线CE是线段AA′的垂直平分线.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目