题目内容
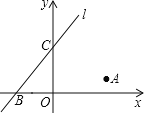
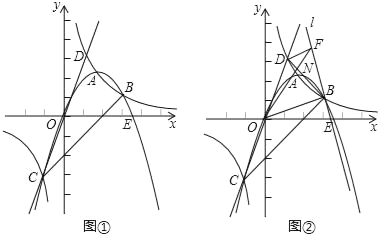
【题目】如图①,双曲线y=![]() (k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图②,过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求![]() 的值.
的值.
【答案】(1)抛物线的解析式为:![]() ,双曲线的解析式为:y=
,双曲线的解析式为:y=![]() .(2)存在点P(
.(2)存在点P(![]() ,1),使得∠POE+∠BCD=90°.(3)
,1),使得∠POE+∠BCD=90°.(3)![]() .
.
【解析】
(1)根据抛物线y=ax2+bx(a≠0)过B(3,1),C(﹣1,﹣3),代入计算即可得到抛物线的解析式. 把B(3,1)代入y=![]() (k≠0)计算可得双曲线的解析式.
(k≠0)计算可得双曲线的解析式.
(2)根据B、C点的坐标计算BC所在的直线方程,根据直线方程可得与坐标轴的交点,因此可计算的OM的长度,再计算BO、CO的长度,可得tan∠COM,根据等量替换可得tan∠POE,设P点的横坐标,即可表示纵坐标,进而计算的P点的坐标.
(3)首先根据C点的坐标,计算CO所在直线的解析式,再根据CO所在的直线与双曲线的交点为D,计算D点的坐标,根据B点的坐标计算OB所在直线的斜率,进而计算直线l的解析式,再根据直线l和DF所在的直线交点为F,计算点F的坐标,进而计算DF的长度,再根据相似比例可得![]() .
.
解:(1)∵抛物线y=ax2+bx(a≠0)过B(3,1),C(﹣1,﹣3),
∴![]() ,
,
解得: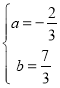 ,
,
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x,
x,
把B(3,1)代入y=![]() (k≠0)得:1=
(k≠0)得:1=![]() ,
,
解得:k=3,
∴双曲线的解析式为:y=![]() .
.
(2)存在点P,使得∠POE+∠BCD=90°;
∵B(3,1),C(﹣1,﹣3),设直线BC为y=kx+n,
∴![]() ,
,
解得k=1,n=﹣2,
∴直线BC为:y=x﹣2,
∴直线BC与坐标轴的交点(2,0),(0,﹣2),
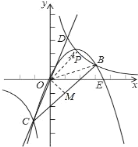
过O作OM⊥BC,则OM=![]() ,
,
∵B(3,1),C(﹣1,﹣3),
∴OB=OC=![]() ,
,
∴BM=![]()
∴tan∠COM=![]() ,
,
∵∠COM+∠BCD=90°,∠POE+∠BCD=90°,
∴∠POE=∠COM,
∴tan∠POE=2,
∵P点是抛物线上的点,设P(m,﹣![]() m2+
m2+![]() m),
m),
∴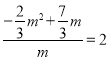 ,
,
解得:m=![]() ,
,
∴P(![]() ,1).
,1).
综上所述,存在点P(![]() ,1),使得∠POE+∠BCD=90°.
,1),使得∠POE+∠BCD=90°.
(3)∵直线CO过C(﹣1,﹣3),
∴直线CO的解析式为y=3x,
解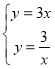 ,
,
解得![]() ,
,
∴D(1,3),
∵B(3,1),
∴直线OB的斜率=![]() ,
,
∵直线l⊥OB,过点D作DF⊥l于点F,
∴DF∥OB,
∴直线l的斜率=﹣3,直线DF的斜率=![]() ,
,
∵直线l过B(3,1),直线DF过D(1,3),
∴直线l的解析式为y=﹣3x+10,直线DF解析式为y=![]() x+
x+![]() ,
,
解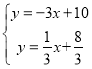 ,
,
解得![]() ,
,
∴F(![]() ,
,![]() ),
),
∴DF=![]() =
=![]() ,
,
∵DF∥OB,OB=![]() ,
,
∴△DNF∽△BNO,
∴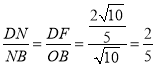 .
.