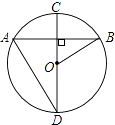
��Ŀ����
����Ŀ���������ϣ�O��ʾԭ�㣬A��B����ֱ��ʾ��8��2��
(1)����߶�AB�ij��ȣ�
(2)����P��A���������������˶����ٶ�Ϊÿ��5����λ���ȣ�ͬʱ��Q��B�����������������˶����ٶ�Ϊÿ��3����λ���ȣ���P��Q�غ�ʱ������ͬʱֹͣ�˶����������˶�ʱ��Ϊt�룬�ú���t��ʽ�ӱ�ʾ�߶�PQ�ij���
(3)��(2)�������£�tΪ��ֵʱ����P����Q��ԭ��O�ľ�����ȣ�

���𰸡�(1)AB��10��(2) PQ��10��2t��0��t��5��(3)Ϊ0.75��5ʱ����P����Q��ԭ��O�ľ�����ȣ�
��������
��1���õ�A��ԭ��O�ľ�����ϵ�B��ԭ��O�ľ��룬��������߶�AB�ij��ȣ�
��2�����߶�AB�ij��ȼ�ȥ����P�����˶��ij��ȣ��ټ��϶���Q�����˶��ij��ȣ��ú���t�Ĵ���ʽ��ʾ�߶�PQ�ij����ɣ�
��3���������⣬������������ٵ�P����Q�غ�ʱ���ڵ�P����Q��ԭ��O������ʱ�����tΪ��ֵʱ����P����Q��ԭ��O�ľ�����ȼ��ɣ�
(1)AB��OA+OB��8+2��10,
(2)PQ��10��5t+3t��10��2t,
��10��2t��0��
���0��t��5��
(3)����P����Q�غ�ʱ��
��10��2t��0��
���t��5��
����P����Q��ԭ��O������ʱ��
OP��8��5t,
OQ��2+3t,
��8��5t��2+3t,
���t��0.75,
����tΪ0.75��5ʱ����P����Q��ԭ��O�ľ�����ȣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij���ξ������Ʊ�۸����±���
��Ʊ��������λ�ˣ� | 1��50 | 51��100 | 100���� |
ÿ����Ʊ�ۣ���λԪ�� | 80 | 75 | 70 |
ij������ƻ����ס������������Ź�100���˼ƻ�ȥ�����þ��㣬���м���������������50�ˣ���������������50 ���˵�����100�ˣ�����������Ŷ��Ը�������Ϊ��λ������Ʊ����һ��֧��7965Ԫ�����������������������Ϊһ�����幺Ʊ����ֻ�ܻ���7210Ԫ�����������Ÿ��ж����ˣ�
����Ŀ����3.15��ֲ���ڻ��ijУ�����µļס��ҡ��������ĸ�Ʒ�ֵ�������гɻ��ʹ۲⣬�����Ǹ��ݹ۲������Ƴɵ�ͳ��ͼ����һ���֣� ��1�����µĸ�Ʒ���������ͳ�Ʊ���
ֲ��Ʒ�� | ���� | ���� | ���� | ���� |
ֲ������ | 150 | 125 | 125 |
�������������Ϣ����������⣺
��1��������µ��ĸ�Ʒ�ֵ����繲�ã���Ʒ�������ã�
��2��ͼ1�У���%����%��
��3����֪��������ɻ���Ϊ90%����ͼ2����������