题目内容
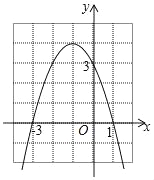
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;②4a+2b+c<0;③一元二次方程ax2+bx+c=1的两根之和为﹣2;④使y≤3成立的x的取值范围是x≥0;⑤抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<﹣1<x2,且x1+x2>﹣2,则y1<y2其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
①求出二次函数的解析式,根据抛物线的顶点坐标确定二次三项式ax2+bx+c的最大值;
②根据x=2时,y<0确定4a+2b+c的符号;
③根据抛物线的对称性确定一元二次方程ax2+bx+c=1的两根之和;
④根据函数图象确定使y≤3成立的x的取值范围.
⑤根据图像即可判断.
解:①根据题意得: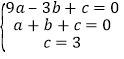 ,
,
解得:a=-1,b=-2,c=3,
∴y=-x2-2x+3=-(x+1)2+4,
∴二次函数图象的顶点坐标为(-1,4),
∴二次三项式ax2+bx+c的最大值为4,故①正确;
②∵当x=2时,y<0,
∴4a+2b+c<0,故②正确;
③∵抛物线与x轴的交点分别是(-3,0),(1,0),
∴一元二次方程ax2+bx+c=0的两根之和=-3+1=-2,故③正确;
④由函数图象可知,当y≤3时,x≥0或x≤-2,故④错误.
⑤根据图形可得当x1<﹣1<x2,且x1+x2>﹣2,y1不一定小于y2,故⑤错误.
故选C.

【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?