题目内容
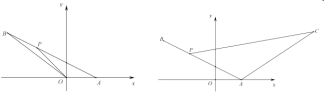
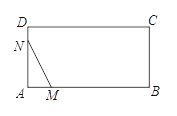
【题目】如图,在矩形ABCD中,AB=4cm,AD=2cm,动点M自点A出发沿A→B的方向,以每秒1cm的速度运动,同时动点N自点A出发沿A→D→C的方向以每秒2cm的速度运动,当点N到达点C时,两点同时停止运动,设运动时间为x(秒),△AMN的面积为y(cm2),则下列图象中能反映y与x之间的函数关系的是( )
A.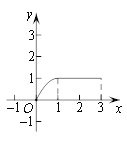 B.
B.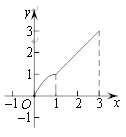 C.
C.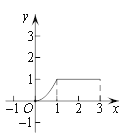 D.
D.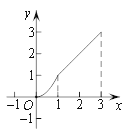
【答案】D
【解析】
根据动点移动是图形的面积变化,确定是属于哪一种函数,再选择图象.
在矩形ABCD中,AB=4cm,AD=2cm,
AD+DC=AB+AD=4+2=6cm,
∵点M以每秒1cm的速度运动,
∴4÷1=4秒,
∵点N以每秒2cm的速度运动,
∴6÷2=3秒,
∴点N先到达终点,运动时间为3秒,
①点N在AD上运动时,y=![]() AMAN=
AMAN=![]() x2x=x2(0≤x≤1);
x2x=x2(0≤x≤1);
②点N在DC上运动时,y=![]()
AMAD=![]() x×2=x(1≤x≤3),
x×2=x(1≤x≤3),
∴能反映y与x之间的函数关系的是D选项.
故选D.

练习册系列答案
相关题目