题目内容
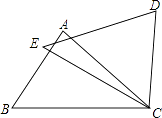
【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE. 
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
【答案】
(1)证明:∵△ABC、△DCE为等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=∠DBC=60°,
∵∠ACD+∠ACB=∠DCB,∠ECD+∠ACD=∠ECA,
∴∠ECA=∠DCB,
在△ECA和△DCB中,
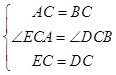 ,
,
∴△ECA≌△DCB(SAS);
(2)解:∵△ECA≌△DCB,
∴∠EAC=∠DBC=60°,
又∵∠ACB=∠DBC=60°,
∴∠EAC=∠ACB=60°,
∴AE∥BC.
【解析】(1)根据等边三角形各内角为60°和各边长相等的性质可证∠ECA=∠DCB,AC=BC,EC=DC,即可证明△ECA≌△DCB;(2)根据△ECA≌△DCB可得∠EAC=60°,根据内错角相等,平行线平行即可解题.
【考点精析】解答此题的关键在于理解平行线的判定的相关知识,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目