题目内容
已知二次函数图象的顶点在原点 ,对称轴为
,对称轴为 轴.一次函数
轴.一次函数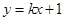 的图象与二次函数的图象交于
的图象与二次函数的图象交于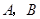 两点(
两点( 在
在 的左侧),且
的左侧),且 点坐标为
点坐标为 .平行于
.平行于 轴的直线
轴的直线 过
过 点.
点.

(1)求一次函数与二次函数的解析式;
(2)判断以线段 为直径的圆与直线
为直径的圆与直线 的位置关系,并给出证明;
的位置关系,并给出证明;
(3)把二次函数的图象向右平移 个单位,再向下平移
个单位,再向下平移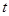 个单位
个单位 ,二次函数的图象与
,二次函数的图象与 轴交于
轴交于 两点,一次函数图象交
两点,一次函数图象交 轴于
轴于 点.当
点.当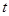 为何值时,过
为何值时,过 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?
 ,对称轴为
,对称轴为 轴.一次函数
轴.一次函数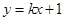 的图象与二次函数的图象交于
的图象与二次函数的图象交于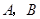 两点(
两点( 在
在 的左侧),且
的左侧),且 点坐标为
点坐标为 .平行于
.平行于 轴的直线
轴的直线 过
过 点.
点.
(1)求一次函数与二次函数的解析式;
(2)判断以线段
 为直径的圆与直线
为直径的圆与直线 的位置关系,并给出证明;
的位置关系,并给出证明;(3)把二次函数的图象向右平移
 个单位,再向下平移
个单位,再向下平移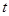 个单位
个单位 ,二次函数的图象与
,二次函数的图象与 轴交于
轴交于 两点,一次函数图象交
两点,一次函数图象交 轴于
轴于 点.当
点.当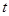 为何值时,过
为何值时,过 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少? (1)把
(1)把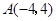 代入
代入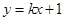 得
得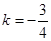 ,
,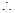 一次函数的解析式为
一次函数的解析式为 ;
; 二次函数图象的顶点在原点,对称轴为
二次函数图象的顶点在原点,对称轴为 轴,
轴, 设二次函数解析式为
设二次函数解析式为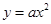 ,
,把
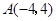 代入
代入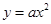 得
得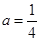 ,
,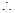 二次函数解析式为
二次函数解析式为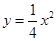 .
.(2)由
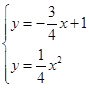
解得
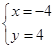 或
或 ,
,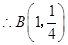 ,
,过
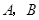 点分别作直线
点分别作直线 的垂线,垂足为
的垂线,垂足为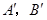 ,
,则
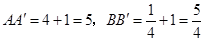 ,
,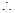 直角梯形
直角梯形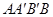 的中位线长为
的中位线长为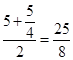 ,
,过
 作
作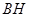 垂直于直线
垂直于直线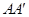 于点
于点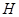 ,则
,则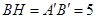 ,
,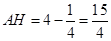 ,
,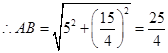 ,
,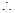
 的长等于
的长等于 中点到直线
中点到直线 的距离的2倍,
的距离的2倍,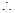 以
以 为直径的圆与直线
为直径的圆与直线 相切.
相切.(3)平移后二次函数解析式为
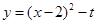 ,
,令
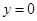 ,得
,得 ,
,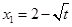 ,
,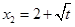 ,
,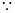 过
过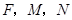 三点的圆的圆心一定在直线
三点的圆的圆心一定在直线 上,点
上,点 为定点,
为定点,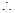 要使圆面积最小,圆半径应等于点
要使圆面积最小,圆半径应等于点 到直线
到直线 的距离,
的距离,此时,半径为2,面积为
 ,
,设圆心为
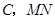 中点为
中点为 ,连
,连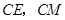 ,则
,则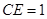 ,
,在三角形
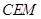 中,
中, ,
,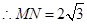 ,而
,而 ,
,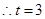 ,
,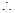 当
当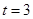 时,过
时,过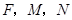 三点的圆面积最小,最小面积为
三点的圆面积最小,最小面积为 .
.说明:本答案解答题中解法只给出了1种或2种,其它解法只要步骤合理、解答正确均应得到相应分数.
(1)已知了一次函数的图象经过A点,可将A点的坐标代入一次函数中,即可求出一次函数的解析式.由于抛物线的顶点为原点,因此可设其解析式为y=ax2,直接将A点的坐标代入抛物线中即可求出抛物线的解析式;
(2)求直线与圆的位置关系需知道圆心到直线的距离和圆的半径长.由于直线l平行于x轴,因此圆心到直线l的距离为1.因此只需求出圆的半径,也就是求AB的长,根据(1)中两函数的解析式即可求出B点的坐标,根据A、B两点的坐标即可求出AB的长.然后判定圆的半径与1的大小关系即可;
(3)先设出平移后抛物线的解析式,不难得出平移后抛物线的对称轴为x=2.因此过F,M,N三点的圆的圆心必在直线x=2上,要使圆的面积最小,那么圆心到F点的距离也要最小(设圆心为C),即F,C两点的纵坐标相同,因此圆的半径就是2.C点的坐标为(2,1)(可根据一次函数的解析式求出F点的坐标).可设出平移后的抛物线的解析式,表示出MN的长,如果设对称轴与x轴的交点为E,那么可表示出ME的长,然后在直角三角形MEC中根据勾股定理即可确定平移的距离.即t的值.(也可根据C点的坐标求出M,N点的坐标,然后用待定系数法求出平移后的抛物线的解析式,经过比较即可得出平移的距离,即t的值).
(2)求直线与圆的位置关系需知道圆心到直线的距离和圆的半径长.由于直线l平行于x轴,因此圆心到直线l的距离为1.因此只需求出圆的半径,也就是求AB的长,根据(1)中两函数的解析式即可求出B点的坐标,根据A、B两点的坐标即可求出AB的长.然后判定圆的半径与1的大小关系即可;
(3)先设出平移后抛物线的解析式,不难得出平移后抛物线的对称轴为x=2.因此过F,M,N三点的圆的圆心必在直线x=2上,要使圆的面积最小,那么圆心到F点的距离也要最小(设圆心为C),即F,C两点的纵坐标相同,因此圆的半径就是2.C点的坐标为(2,1)(可根据一次函数的解析式求出F点的坐标).可设出平移后的抛物线的解析式,表示出MN的长,如果设对称轴与x轴的交点为E,那么可表示出ME的长,然后在直角三角形MEC中根据勾股定理即可确定平移的距离.即t的值.(也可根据C点的坐标求出M,N点的坐标,然后用待定系数法求出平移后的抛物线的解析式,经过比较即可得出平移的距离,即t的值).

练习册系列答案
相关题目
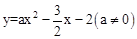 的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).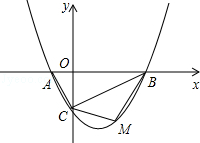
 的图象与x轴和y轴分别交于点A(6,0)和B(0,
的图象与x轴和y轴分别交于点A(6,0)和B(0, ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.
 的坐标分别为
的坐标分别为 .
. ,使得
,使得 关于点
关于点 成中心对称;
成中心对称;
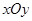 中,半径为1的圆的圆心
中,半径为1的圆的圆心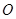 在坐标原点,且与两坐标轴分别交于
在坐标原点,且与两坐标轴分别交于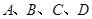 四点.抛物线
四点.抛物线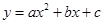 与
与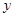 轴交于点
轴交于点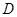 ,与直线
,与直线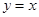 交于点
交于点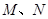 ,且
,且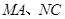 分别与圆
分别与圆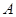 和点
和点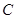 .
.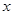 轴于点
轴于点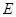 ,连结
,连结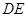 ,并延长
,并延长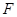 ,求
,求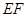 的长.
的长.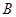 作圆
作圆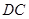 的延长线于点
的延长线于点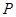 ,判断点
,判断点
 的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线
的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线
 的二次函数
的二次函数 与
与 ,当
,当 时,
时, ;且二次函数
;且二次函数 的图象的对称轴是直线
的图象的对称轴是直线 .
. 的值;
的值; 的表达式;
的表达式;