题目内容
已知两个关于 的二次函数
的二次函数 与
与 ,当
,当 时,
时, ;且二次函数
;且二次函数 的图象的对称轴是直线
的图象的对称轴是直线 .
.
(1)求 的值;
的值;
(2)求函数 的表达式;
的表达式;
(3)在同一直角坐标系内,问函数 的图象与
的图象与 的图象是否有交点?请说明理由.
的图象是否有交点?请说明理由.
 的二次函数
的二次函数 与
与 ,当
,当 时,
时, ;且二次函数
;且二次函数 的图象的对称轴是直线
的图象的对称轴是直线 .
.(1)求
 的值;
的值;(2)求函数
 的表达式;
的表达式;(3)在同一直角坐标系内,问函数
 的图象与
的图象与 的图象是否有交点?请说明理由.
的图象是否有交点?请说明理由.(1)由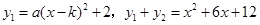
得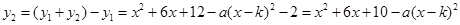 .
.
又因为当 时,
时, ,即
,即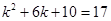 ,
,
解得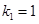 ,或
,或 (舍去),故
(舍去),故 的值为
的值为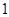 .
.
(2)由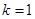 ,得
,得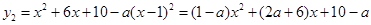 ,
,
所以函数 的图象的对称轴为
的图象的对称轴为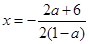 ,
,
于是,有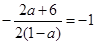 ,解得
,解得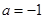 ,
,
所以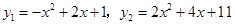 .
.
(3)由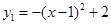 ,得函数
,得函数 的图象为抛物线,其开口向下,顶点坐标为
的图象为抛物线,其开口向下,顶点坐标为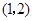 ;
;
由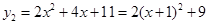 ,得函数
,得函数 的图象为抛物线,其开口向上,顶点坐标为
的图象为抛物线,其开口向上,顶点坐标为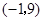 ;
;
故在同一直角坐标系内,函数 的图象与
的图象与 的图象没有交点.
的图象没有交点.
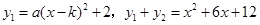
得
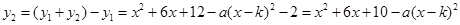 .
. 又因为当
 时,
时, ,即
,即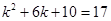 ,
, 解得
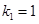 ,或
,或 (舍去),故
(舍去),故 的值为
的值为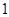 .
. (2)由
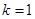 ,得
,得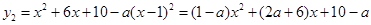 ,
, 所以函数
 的图象的对称轴为
的图象的对称轴为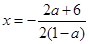 ,
, 于是,有
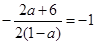 ,解得
,解得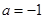 ,
, 所以
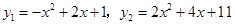 .
. (3)由
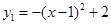 ,得函数
,得函数 的图象为抛物线,其开口向下,顶点坐标为
的图象为抛物线,其开口向下,顶点坐标为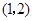 ;
;由
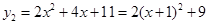 ,得函数
,得函数 的图象为抛物线,其开口向上,顶点坐标为
的图象为抛物线,其开口向上,顶点坐标为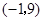 ;
; 故在同一直角坐标系内,函数
 的图象与
的图象与 的图象没有交点.
的图象没有交点. (1)先根据题意求得 的关系式,当
的关系式,当 时,
时, ,即可求得
,即可求得 的值;
的值;
(2)由(1)得到k的值,再由二次函数 的图象的对称轴是直线
的图象的对称轴是直线 即可求得a的值;
即可求得a的值;
根据函数 、
、 的解析式即可得到图象的特征,从而可以判断出是否有交点。
的解析式即可得到图象的特征,从而可以判断出是否有交点。
 的关系式,当
的关系式,当 时,
时, ,即可求得
,即可求得 的值;
的值;(2)由(1)得到k的值,再由二次函数
 的图象的对称轴是直线
的图象的对称轴是直线 即可求得a的值;
即可求得a的值;根据函数
 、
、 的解析式即可得到图象的特征,从而可以判断出是否有交点。
的解析式即可得到图象的特征,从而可以判断出是否有交点。
练习册系列答案
相关题目
 ,对称轴为
,对称轴为 轴.一次函数
轴.一次函数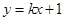 的图象与二次函数的图象交于
的图象与二次函数的图象交于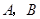 两点(
两点( 在
在 的左侧),且
的左侧),且 .平行于
.平行于 轴的直线
轴的直线 过
过 点.
点.
 为直径的圆与直线
为直径的圆与直线 个单位,再向下平移
个单位,再向下平移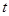 个单位
个单位 ,二次函数的图象与
,二次函数的图象与 两点,一次函数图象交
两点,一次函数图象交 点.当
点.当 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少? 经过(-1,0),(0,-3),(2,-3)三点.
经过(-1,0),(0,-3),(2,-3)三点. 与
与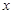 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当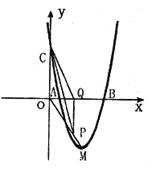
 、
、 ,-1,0、1、3的6张卡片,背面完全相同,洗匀后,从中任取两张,该卡片上的数分别作为点P 的横坐标和纵坐标,P落在抛物线
,-1,0、1、3的6张卡片,背面完全相同,洗匀后,从中任取两张,该卡片上的数分别作为点P 的横坐标和纵坐标,P落在抛物线 与对称轴右侧所围成的区域内(不含边界)的概率是 。
与对称轴右侧所围成的区域内(不含边界)的概率是 。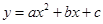 图象的一部分,图象过
图象的一部分,图象过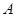 点(3,0),二次函数图象对称轴为
点(3,0),二次函数图象对称轴为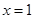 ,给出四个结论:①
,给出四个结论:①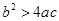 ;②
;②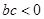 ;③
;③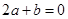 ;④
;④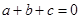 ,其中正确结论是( )
,其中正确结论是( )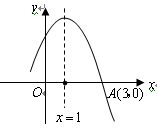
 (单位:米)与小球运动时间
(单位:米)与小球运动时间 (单位:秒)的函数关系式是
(单位:秒)的函数关系式是 ,那么小球运动中的最大高度
,那么小球运动中的最大高度 .
.