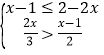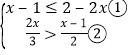题目内容
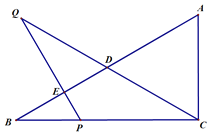
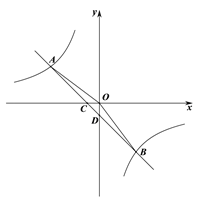
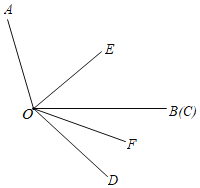
【题目】如图,点![]() 是直线
是直线![]() 上任一点,射线
上任一点,射线![]() 和射线
和射线![]() 分别平分
分别平分![]() 和
和![]() .
.
(1)填空:与![]() 互补的角有______;
互补的角有______;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)当![]() 时,请直接写出
时,请直接写出![]() 的度数.
的度数.
【答案】(1)∠AOD、∠COD;(2)90°;(3)90°.
【解析】
(1)先根据角平分线的定义得出∠AOD=∠COD,再由∠AOD+∠BOD=180°,即可得出答案;
(2)根据补角的定义和角平分线的定义求出∠COE,即可得出∠DOE;
(3)根据角平分线的定义和补角的定义依次求出∠EOC和∠DOC,即可得出∠DOE.
解:(1)∵OD平分∠AOC,∴∠AOD=∠COD;
∵∠AOD+∠BOD=180°,∴∠COD+∠BOD=180°,
∴与∠BOD互补的角是∠AOD和∠COD;
故答案为∠AOD、∠COD;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=26°,∠COE=∠BOE=![]() ∠BOC,
∠BOC,
∴∠AOC=2×26°=52°,∴∠BOC=180°-52°=128°,
∴∠COE=![]() ∠BOC=64°,
∠BOC=64°,
∴∠DOE=∠COD+∠COE=90°;
(3)当![]() 时,∠DOE=90°.
时,∠DOE=90°.
理由:∵OE平分∠BOC,∴∠COE=∠BOE=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠BOC=2![]() ,∴
,∴![]() ,
,
∵OD平分∠AOC,∴∠COD =![]() ∠AOC=
∠AOC=![]() ,
,
∴∠DOE=∠EOC+∠DOC=![]() +
+![]() =
=![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】观察表格:
|
|
| |
1条直线 0个交点 平面分成(1+1)块 | 2条直线 1个交点 平面分成(1+1+2)块 | 3条直线 (1+2)个交点 平面分成(1+1+2+3)块 | 4条直线 (1+2+3)个交点 平面分成(1+1+2+3+4)块 |
根据表格中的规律解答问题:
(1)5条直线两两相交,有 个交点,平面被分成 块;
(2)n条直线两两相交,有 个交点,平面被分成 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 块饼.