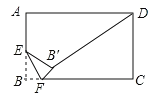
题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的动点,连结
边上的动点,连结![]() .
.
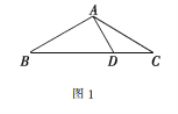
(1)如图,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
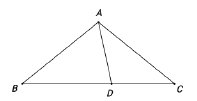
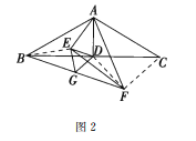
(2)如图,若![]() ,
,![]() 是
是![]() 的中点,把
的中点,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度(
度(![]() )后得到
)后得到![]() ,连结
,连结![]() ,点
,点![]() 是
是![]() 中点.求证:
中点.求证:![]() 是等边三角形.
是等边三角形.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)证明△ADC∽△BAC,通过比例式进行求解;
(2)连接BE、DF、CF,根据三角函数得出∠CAD=∠BAD=60°,先后证明△BAE≌△FAD、△EBG≌△DFG,利用等边三角形的判定方法说明△DEG是等边三角形.
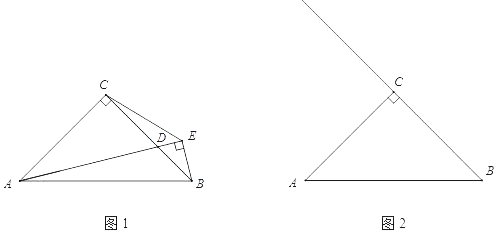
(1)如图1,在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
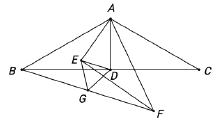
(2)如图2,连结![]() 、
、![]() 、
、![]() ,
,
∵![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() 后得到
后得到![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目