题目内容
【题目】直线y= ![]() x与双曲线y=
x与双曲线y= ![]() 的交点A的横坐标为2
的交点A的横坐标为2
(1)求k的值
(2)如图,过点P(m,3)(m>0)作x轴的垂线交双曲线y= ![]() (x>0)于点M,交直线OA于点N
(x>0)于点M,交直线OA于点N 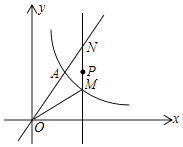
①连接OM,当OA=OM时,直接写出PN﹣PM的值
②试比较PM与PN的大小,并证明你的结论.
【答案】
(1)解:∵点A在直线y= ![]() x上,且A点的横坐标为2,
x上,且A点的横坐标为2,
∴y= ![]() ×2=3,
×2=3,
∴A(2,3),把A(2,3)代入y= ![]() ,可得k=6,
,可得k=6,
∴k=6.
(2)解:①当M与A重合时,PN﹣PM=0,
当M(3,2)时,P(3,3),N(3, ![]() ),
),
∴PN﹣PM=( ![]() ﹣3)﹣(3﹣2)=
﹣3)﹣(3﹣2)= ![]() ,
,
综上所述PN﹣PM=0或 ![]() .
.
②∵PM⊥x轴,P(m,3),
∴N(3, ![]() m),M(m,
m),M(m, ![]() ).
).
∴PN=| ![]() m﹣3|,PM=|
m﹣3|,PM=| ![]() ﹣3|,
﹣3|,
当P、M、N三点重合时,PM=PM=0.
当0<m<2时,PM= ![]() ﹣3,PN=3﹣
﹣3,PN=3﹣ ![]() m,
m,
PM﹣PN= ![]() ﹣3﹣(3﹣
﹣3﹣(3﹣ ![]() m)=
m)= ![]() ﹣6+
﹣6+ ![]() m=6(
m=6( ![]() ﹣
﹣ ![]() )2>0,
)2>0,
∴PM>PN.
当m>2时,PM=3﹣ ![]() ,PN=
,PN= ![]() m﹣3,
m﹣3,
PM﹣PN=3﹣ ![]() ﹣(
﹣( ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() +6﹣
+6﹣ ![]() m=﹣6(
m=﹣6( ![]() ﹣
﹣ ![]() )2<0,
)2<0,
∴PM<PN,
综上所述,当m=2时,PM=PN,当0<m<2时,PM>PN,当m>2时,PM<PN.
【解析】(1)先求出点A坐标,利用待定系数法即可解决问题.(2)①分两种情形讨论求解.②分三种情形讨论求解a、m=2.b、0<m<2,C、m>2.分别利用求差法比较大小即可.

练习册系列答案
相关题目