��Ŀ����
��ͼ1����ƽ��ֱ������ϵxOy�У���MΪ������ �Ķ��㣬���㣨0��4����x���ƽ���ߣ����������ڵ�P��Q����P��Q����ࣩ��PQ=4��
�Ķ��㣬���㣨0��4����x���ƽ���ߣ����������ڵ�P��Q����P��Q����ࣩ��PQ=4��
��1���������ߵĺ�����ϵʽ����д����P�����ꣻ
��2��С�����֣��������� ���ŵ�P��ת180�㣬�����������ߵĶ���ǡΪ����ԭ��O������Ϊ��ȷ����˵�����ɣ�
���ŵ�P��ת180�㣬�����������ߵĶ���ǡΪ����ԭ��O������Ϊ��ȷ����˵�����ɣ�
��3����ͼ2����֪��A��1��0������PAΪ��������PABC����P��A��B��C��˳ʱ��ķ������У��� ��
��
��д��C������꣺C�� �� ���������ú���t�Ĵ���ʽ��ʾ����
������C���⣨2������ת������������ϣ���t��ֵ��
��1��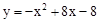 ����2��4������2����ȷ�����ɼ���������3����-4t+2��4+t����
����2��4������2����ȷ�����ɼ���������3����-4t+2��4+t���� .
.
���������������1����P����������������ߵĽ���ʽ�õ�����x�ķ��̣����ݸ���ϵ���Ĺ�ϵ��ú�PQ=4�����n��ֵ��������ý���ʽ.
��2��������ת�����ʵõ�Q���ŵ�P��ת180���ĶԳƵ�ΪQ�䣨-2��4�����ó��������ߵĶԳ�����y�ᣬȻ����������ߵĶ��㵽ֱ��PQ�ľ���Ϊ4�������ж��������߶���ӦΪ����ԭ�㣮
��3���ٸ������������Ƽ������C�����꣺
���ͼ����P��x��Ĵ��ߣ���x����M����C��CN��MN��N��
�� ����
����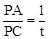 .
.
���á�APM�ס�PCN����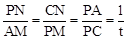 .
.
��AM=2-1=1��PM=4����PN=t��CN=4t.
��MN=4+t.
��C��-4t+2��4+t����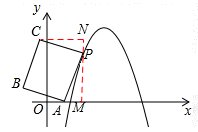
���ɣ�1����֪����ת�������������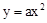 ������������
������������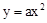 ��P��2��4��������������ߵĽ���ʽ����C��-4t+2��4+t�����뼴�����t��ֵ��
��P��2��4��������������ߵĽ���ʽ����C��-4t+2��4+t�����뼴�����t��ֵ��
����������⣺��1���������� ����P��P���������Ϊ4��
����P��P���������Ϊ4��
��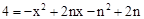 ��
��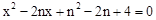 .
.
��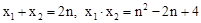 .
.
��PQ=4����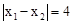 ����
����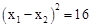 ����
����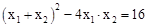 .
.
��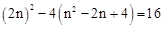 ����ã�n=4.
����ã�n=4.
�������ߵĺ�����ϵʽΪ��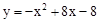 .
.
��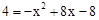 ���x=2��x=6.
���x=2��x=6.
��P��2��4����
��2����ȷ���������£�
��P��2��4����PQ=4����Q���ŵ�P��ת180���ĶԳƵ�ΪQ�䣨-2��4��.
��P��Q�����ù���y��Գ�.
�������������ߵĶԳ�����y�ᣬ
��������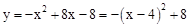 ���������ߵĶ���M��4��8��.
���������ߵĶ���M��4��8��.
�ඥ��M��ֱ��PQ�ľ���Ϊ4.
�������������߶��㵽ֱ��PQ�ľ���Ϊ4.
�������������߶���ӦΪ����ԭ�㣮
��3����-4t+2��4+t.
���ɣ�1����֪����ת�������������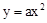 ��
��
����������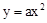 ��P��2��4������4=4a�����a=1.
��P��2��4������4=4a�����a=1.
����ת�������������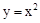 .
.
��C��-4t+2��4+t����������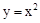 �ϣ�
�ϣ�
�� ����ã�t=0����ȥ����t=
����ã�t=0����ȥ����t= .
.
��t= .
.
���㣺1.���κ����ۺ��⣻2.�߶���ת���⣻3.�����ϵ�������뷽�̵Ĺ�ϵ��4.һԪ���η��̸���ϵ���Ĺ�ϵ��5.���κ��������ʣ�6. ��ת����ԳƵ����ʣ�7.����˼���Ӧ��.

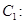
 ��
�� �ύ�ڵ�
�ύ�ڵ� ��
�� ����
���� ����ƽ�Ƶõ�2��������
����ƽ�Ƶõ�2�������� ����
���� ���ٽ�
���ٽ� ����
���� ���ֽ�
���ֽ� ����
���� ����
���� ��
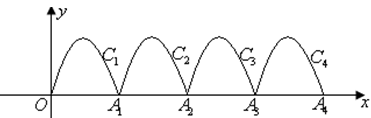
�� ��ֵ�� ��
��ֵ�� ��
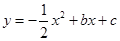 ͼ��A��-1��0����B��4��0�����㣮
ͼ��A��-1��0����B��4��0�����㣮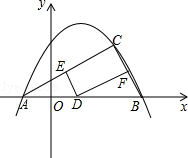
 ��
�� ���
��� ��ֱ���A��B���㣬���κ���
��ֱ���A��B���㣬���κ��� ��ͼ����A��B���Ҷ���ΪC��
��ͼ����A��B���Ҷ���ΪC��
 ��ֵ��
��ֵ��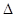 ABP�����Ϊ10�����P�����꣮
ABP�����Ϊ10�����P�����꣮

 ��������
�������� ����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8.
����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8.