题目内容
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A、C分别在x轴、y轴的正半轴上,抛物线L经过0、P、A三点,点E是正方形内的抛物线上的动点.
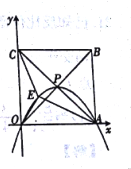
(1)点P的坐标为______
(2)求抛物线L的解析式.
(3)求△OAE与△OCE的面积之和的最大值.
【答案】(1)(2,2);(2)![]() ;(3)9.
;(3)9.
【解析】试题分析:(1)根据正方形的边长结合正方形的性质即可得出点![]() 三点的坐标;
三点的坐标;
(2)设抛物线L的解析式为![]() 结合点
结合点![]() 的坐标利用待定系数法即可求出抛物线的解析式;
的坐标利用待定系数法即可求出抛物线的解析式;
(3)由点![]() 为正方形内的抛物线上的动点,设出点
为正方形内的抛物线上的动点,设出点![]() 的坐标,结合三角形的面积公式找出
的坐标,结合三角形的面积公式找出![]() 关于
关于![]() 的函数解析式,根据二次函数的性质即可得出结论.
的函数解析式,根据二次函数的性质即可得出结论.
试题解析:(1)∵OABC为正方形,且边长为4,对角线相交于点P,
∴点O的坐标为(0,0),点B的坐标为(4,4),点P为OB的中点,
∴点P的坐标为(2,2).
故答案为:(2,2).
(2)设抛物线L的解析式为![]()
∵抛物线L经过O、P、A三点,
∴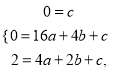 解得:
解得: 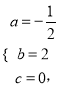
∴抛物线L的解析式为![]()
(3)∵点E是正方形内的抛物线上的动点,
∴设点E的坐标为![]()
∴![]()
∴当m=3时,△OAE与△OCE面积之和最大,最大值为9.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目