题目内容
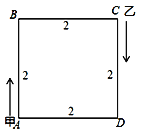
【题目】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法:把两个全等的直角三角形如图1放置,其三边长分别为a、b、c,显然∠DAB=∠B=90°,AC⊥DE.
(1)请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再通过探究这三个图形面积之间的关系,证明:勾股定理a2+b2=c2;
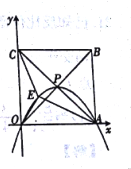
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,在AB上有一个供应站P,且PC=PD,求出AP的距离;
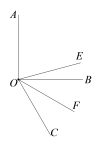
(3)借助(2)的思考过程与几何模型,直接写出代数式![]() 的最小值为 .
的最小值为 .

【答案】(1)见解析;(2)16千米;(3)20 .
【解析】
(1)表示出三个图形的面积进行加减计算可证a2+b2=c2
(2)以(1)中关于直角三角形的结论和K型模型建立方程关系,解方程可得AP的值
(3)将条件中的数表示为直角三角形的直角边,画对应图形,作轴对称图形,在三点共线时有最小值.
解:(1)梯形ABCD的面积![]()
四边形AECD的面积![]()
△EBC的面积![]()
∵梯形ABCD的面积=四边形AECD的面积+△EBC的面积
∴![]()
∴a2+b2=c2
(2)如图,当DP=PC时
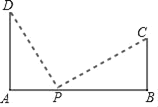
设AP=a,BP=40﹣a
∵DP2=CP2
∴AP2+AD2=BP2+CB2
∴a2+242=(40﹣a)2+162
解得 a=16
∴AP=16千米
(3)如图,![]()
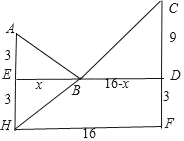
∴AB+BC的最小值即为H、B、C三点共线时
HC=![]() =20
=20
∴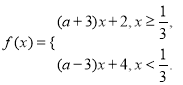 的最小值为20
的最小值为20
故答案为:20

练习册系列答案
相关题目