Question

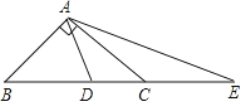
【题目】（1）如图，在△ABC中，∠BAC=90°，AB=AC，点D在BC上，且BD=BA，点E在BC的延长线上且CE=CA，试求∠DAE的度数；

（2））如果把第（1）题中“∠BAC=90°”的条件改为“∠BAC＞90°”，其余条件不变，那么∠DAE与∠BAC有怎样的数量关系？

Answer 1

【答案】见解析

【解析】试题分析：

(1) 要求∠DAE的度数只要得到∠DAC与∠CAE的度数然后求和即可. 分析条件可知，△ABC，△ABD，△ACE均为等腰三角形. ∠B的度数易知，故∠BAD的度数可以在△ABD中由三角形内角和得到，进而可以得到∠DAC的度数. ∠ACB的度数易知，故∠CAE的度数可由三角形的外角关系得到. 这样即可求得∠DAE的度数.

(2) 通观第(1)小题的分析可知，∠DAE的度数实质上是由∠BAC的度数通过运算得到的. 分析本题的几何图形可知，第(2)小题所改变的条件并没有影响各角之间的几何关系. 因此，第(1)小题的思路可以用来求解∠DAE与∠BAC的数量关系. 求解时，参照第(1)小题的思路，将∠BAC当作代表角度的代数符号代入相应的式子进行运算，从而得到∠DAE与∠BAC的数量关系.

试题解析：

(1) ∠DAE=45°. 求解过程如下：

∵在△ABC中，∠BAC=90°，AB=AC，

∴∠B=∠ACB=45°，

∵AB=BD，

∴在△ABD中， ，

∴∠DAC=∠BAC-∠BAD=90°-67.5°=22.5°，

∵∠ACB是△ACE的一个外角，

∴∠ACB=∠CEA+∠CAE，

∵CE=CA，

∴，

∵∠ACB=45°，

∴，

∴∠DAE=∠DAC+∠CAE=22.5°+22.5°=45°.

(2) . 理由如下：

∵在△ABC中，AB=AC，

∴,

∵AB=BD，

∴在△ABD中， ，

∴，

∵∠DAC=∠BAC-∠BAD，

∴，

∵∠ACB是△ACE的一个外角，

∴∠ACB=∠CEA+∠CAE，

∵CE=CA，

∴在△ACE中， ，

∵，

∴，

∴.