Question

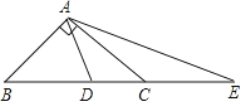
【题目】已知，△ABC、△DCE均为等边三角形，且B、C、E三点在一条直线上，BD与AE相交于O点．

（1）求证：△BCD≌△ACE；

（2）求∠DOE的度数；

（3）连接MN，求证：MN∥BE．

Answer 1

【答案】见解析

【解析】试题分析：

(1) △ABC、△DCE均为等边三角形，易知BC=AC，CD=CE. 这样，对于△BCD与△ACE而言，已经获得了两组对应边的相等关系，只要再证明这两组对应边所夹的角∠BCD与∠ACE对应相等就可以用SAS证明这组三角形全等了.观察图形可知，∠BCD与∠ACE均是由等边三角形的一个内角加上一个相同的角∠ACD而形成的，进而可以证明其相等.

(2) 观察图形可知，∠DOE是△BOE的一个外角，容易联想到用三角形外角的相关结论求解该题. 利用三角形外角的相关结论以及第(1)小题中的全等三角形，可以将∠DOE转化为∠DBC+∠BDC，再由三角形外角的相关结论可知∠DOE与等边三角形内角∠DCE相等，得到答案.

(3) 分析条件可知∠ACN=60°，结合图形的形状可以猜想△MCN为等边三角形. 若△MCN为等边三角形，即可通过“内错角相等，两直线平行”的方法证明MN∥BE. 本题的问题转化为如何证明△MCN为等边三角形. 利用第(1)小题中的全等三角形可以证明△CAN与△CBM全等，得到CN=CM. 这样就证明了△MCN为等边三角形，进而容易证明MN∥BE.

试题解析：

(1) ∵△ABC与△DCE均为等边三角形，

∴BC=AC，CD=CE，∠ACB=∠DCE=60°，

∴∠ACB+∠ACD =∠DCE+∠ACD，即∠BCD=∠ACE，

∵在△BCD与△ACE中：

，

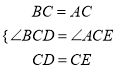∴△BCD≌△ACE (SAS).

(2) ∵∠DOE是△BOE的一个外角，

∴∠DOE=∠OBE+∠OEB，即∠DOE=∠DBC+∠AEC，

∵△BCD≌△ACE，

∴∠BDC=∠AEC，

∴∠DOE=∠DBC+∠BDC，

∵∠DCE是△BCD的一个外角，

∴∠DCE=∠DBC+∠BDC，

∴∠DOE=∠DCE，

∵△DCE为等边三角形，

∴∠DCE=60°，

∴∠DOE=∠DCE=60°.

(3) ∵△ABC与△DCE均为等边三角形，

∴AC=BC，∠ACB=∠DCE=60°，即∠BCM=∠ECN=60°，

∵B、C、E三点在一条直线上，

∴∠ACN+∠BCM+∠ECN=180°，

∴∠ACN=180°-∠BCM-∠ECN=180°-60°-60°=60°，

∴∠ACN=∠BCM，

∵△BCD≌△ACE，

∴∠CBD=∠CAE，即∠CAN=∠CBM，

∵在△CAN与△CBM中：

，

∴△CAN≌△CBM (ASA)，

∴CN=CM，

∵∠ACN=60°且CN=CM，

∴△MCN为等边三角形，

∴∠CMN=60°，

∴∠CMN=∠ACB=60°，

∴MN∥BE.