题目内容
【题目】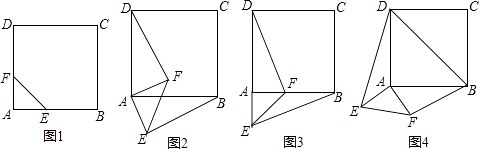
(1)如图1,四边形ABCD是正方形,点E、点F分别在边AB和AD上,且AE=AF.此时,线段BE、DF的数量关系是 , 位置关系是 . 请直接写出结论.
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.
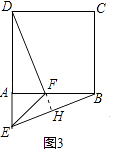
(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当α=90°时,连接BE、DF,若正方形的边长为1,猜想当AE=时,直线DF垂直平分BE.请写出计算过程.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论: .
【答案】
(1)BE=DF;BE⊥DF
(2)
中的结论仍然成立.
理由:如图2中,延长DF交BE于H.
∵四边形ABCD是正方形,
∴AD=AB,AF=AE,∠DAB=∠FAE=90°,
在△DAF和△BAE中,
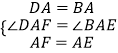 ,
,
∴△DAF≌△BAE,
∴DF=BE,∠ADF=∠ABR,
∵∠AFD=∠BFH,
∴∠DAF=∠BHF=90°,
∴DF⊥BE
(3)![]() ﹣1
﹣1
(4)正方形
【解析】解:(1.)如图1中,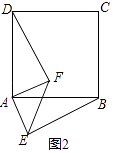
∵四边形ABCD是正方形,
∴∠DAB=90°,AD=AB,
∵AF=AE,
∴BE=DF,BE⊥DF,
所以答案是BE=DF,BE⊥DF
(3.)如图3中,连接BD.
在Rt△ABD中,∵AD=AB=1,
∴BD= ![]() =
= ![]() ,
,
∵DF垂直平分线段EB,
∴DE=DB= ![]() ,
,
∴AE=DE﹣AD= ![]() ﹣1,
﹣1,
所以答案是 ![]() ﹣1.
﹣1.
(4.)如图4中,设M、N、G、H分别是BD、DE、EF、BF的中点,连接BE,DF,MN,NG,GH,HM.EB交DF于O,MN交DF于P.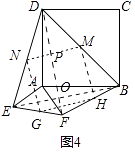
易证:DF=EB,DF⊥EB,
∵DN=NE,DM=MB,
∴MN∥EB,MN= ![]() EB,同理可证GH∥EB,GH=
EB,同理可证GH∥EB,GH= ![]() EB,MH∥DF,MH=
EB,MH∥DF,MH= ![]() DF,GN∥DF,GN=
DF,GN∥DF,GN= ![]() DF,
DF,
∴MN=NG=GH=HM,
∴四边形MNGH是菱形,
∵MN∥EB,
∴∠DPM=∠DOB=90°,
∵DF∥MH,
∴∠NMH=∠DPM=90°,
∴四边形MNGH是正方形.
所以答案是正方形
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案