题目内容
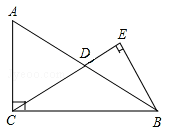
【题目】如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.
(1)若∠AOC= 50°,则∠DOE= °;
(2)若∠AOC= 50°,则图中与∠COD互补的角为 ;
(3)当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?

【答案】(1)90°;(2)∠BOD;(3)不发生改变,理由详见解析.
【解析】
(1)由∠AOC=50°,得到∠AOD=∠COD=25°,∠BOC=130°,求得∠COE=∠BOE=115°.即可求出∠DOE;
(2)由(1)得∠AOD=∠COD=25°,则∠BOD=155°,即可得到答案;
(3)设∠AOC=2x,则∠AOD =∠COD = x,得到∠COE=90°+x,即可得到∠DOE=90°.
解:(1)∵∠AOC=50°,
∴∠BOC=180°![]() 130°,
130°,
∵OD是∠AOC的角平分线,
∴∠AOD=∠COD=25°,
∴∠COE=∠BOE=![]() ,
,
∴∠DOE=115°![]() ;
;
故答案为:90.
(2) 由(1)知∠AOD=∠COD=25°,
∴∠BOD=155°,
∴图中与∠COD互补的角为∠BOD;
故答案为:∠BOD.
(3)不发生改变,
设∠AOC=2x .
∵OD是∠AOC的平分线,
∴∠AOD =∠COD=x,
∴∠BOC=180° 2x,
∵∠COE=∠BOE,
∴∠COE=![]() =90°+x,
=90°+x,
∴∠DOE=90°+x x=90°.

练习册系列答案
相关题目