题目内容
【题目】如图在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=![]() .
.
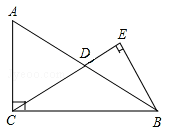
(1)求线段CD的长;
(2)求sin∠DBE的值.
【答案】解:(1)∵在Rt△ABC中,AC=15,cosA=![]() ,∴AB=25。
,∴AB=25。
∵△ACB为直角三角形,D是边AB的中点,∴CD=![]() 。
。
(2)在Rt△ABC中,![]() 。
。
又AD=BD=CD=![]() ,设DE=x,EB=y,则
,设DE=x,EB=y,则
在Rt△BDE中,![]() ①,
①,
在Rt△BCE中,![]() ②,
②,
联立①②,解得x=![]() 。
。
∴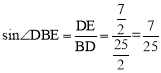 。
。
【解析】(1)根据直角三角形斜边上的中线等于斜边的一半,求出AB的长,即可求出CD的长;
由于D为AB上的中点,求出AD=BD=CD=![]() ,设DE=x,EB=y,利用勾股定理即可求出x的值,据此解答即可。
,设DE=x,EB=y,利用勾股定理即可求出x的值,据此解答即可。

练习册系列答案
相关题目